
2006年廣西貴港市中等學(xué)校招生統(tǒng)一考試(大綱卷)
(考試時間120分鐘,賦分120分)
一、細心填一填:本大題共10小題,每小題2分,共20分.請將答案填寫在題中的橫線上.
1. 的相反數(shù)是 .
的相反數(shù)是 .
2.分解因式: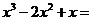 .
.
3.人體中約有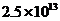 個紅細胞,則
個紅細胞,則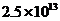 中有 個有效數(shù)字.
中有 個有效數(shù)字.
4.計算: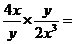 .
.
5.如圖,直線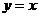 是線段
是線段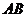 的垂直平分線,若
的垂直平分線,若 點的坐標(biāo)是
點的坐標(biāo)是 ,則
,則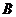 點的坐標(biāo) 是
.
點的坐標(biāo) 是
.
6.在函數(shù)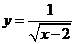 中,自變量
中,自變量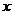 的取值范圍是 .
的取值范圍是 .
7.如圖,在 中,
中,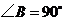 ,
,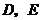 分別是邊
分別是邊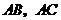 的中點,
的中點,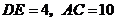 ,則
,則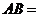 .
.
 |
8.如圖,在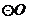 中,弦
中,弦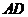 平行于弦
平行于弦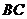 ,若
,若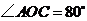 ,則
,則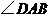 = 度.
= 度.
9.如圖,正六邊形 的邊長為
的邊長為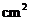 .
.
10.觀察下列各等式: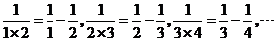
根據(jù)你發(fā)現(xiàn)的規(guī)律,計算: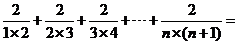 (
(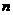 為正整數(shù)).
為正整數(shù)).
二、精心選一選:本大題共8小題,每小題3分,共24分.在每小題給出的四個選項中,只有一個是正確的,請將正確答案前的字母填入題后的括號內(nèi).每小題選對得3分,選錯、不選或多選均得零分.
11.下列計算中,正確的是( )
A.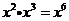 B.
B. C.
C.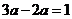 D.
D.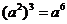
12.已知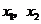 是方程
是方程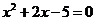 的兩根,則
的兩根,則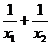 的值為( )
的值為( )
 A.
A. B.
B. C.
C.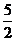 D.
D.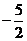
13.如圖, 為
為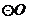 的割線,且
的割線,且 ,
,
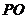 交
交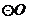 于點
于點 ,若
,若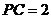 ,則
,則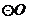 的半徑的
的半徑的
長為( )
A.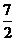 B.
B. C.
C.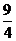 D.7
D.7
14.下列二次根式中,最簡二次根式是( )
A. B.
B. C.
C. D.
D.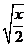
 15.在同一直角坐標(biāo)系中,函數(shù)
15.在同一直角坐標(biāo)系中,函數(shù)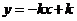 與
與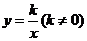 的圖象大致是( )
的圖象大致是( )
16.下列命題:①平行四邊形對角線一定相等;②等腰梯形在同一底上的兩個角相等;③四邊形的內(nèi)角和等于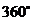 ;④關(guān)于中心對稱的兩個圖形是全等形.其中正確命題的個數(shù)有( )
;④關(guān)于中心對稱的兩個圖形是全等形.其中正確命題的個數(shù)有( )
 A.1個 B.2個 C.3個 D.4個
A.1個 B.2個 C.3個 D.4個
17.如圖,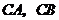 分別與
分別與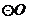 相切于點
相切于點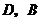 ,圓心
,圓心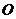 在
在
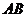 上,
上,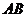 與
與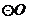 的另一交點為
的另一交點為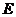 ,
,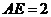 ,
,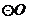 的半徑
的半徑
為1,則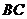 的長為( )
的長為( )
A.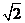 B.
B.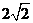 C.
C.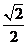 D.
D.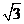
18.已知菱形的周長為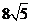 ,面積為
,面積為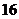 ,則這個菱形較短的對角線長為( )
,則這個菱形較短的對角線長為( )
A.4 B.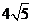 D.10
D.10
三、解答題:本大題共8小題,滿分76分.
19.計算下列各題(本題滿分11分,第(1)題5分,第(2)題6分)
(1)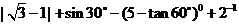
(2)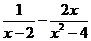
20.(本題滿分8分)
我市某初中舉行“八榮八恥”知識搶答賽,總共50道搶答題.搶答規(guī)定:搶答對1題得3分,搶答錯1題扣1分,不搶答得0分.小軍參加了搶答比賽,只搶答了其中的20道題,要使最后得分不少于50分,問小軍至少要答對幾道題?
21.(本題滿分8分)
如圖, ,
,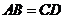 ,點
,點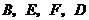 在同一直線上,
在同一直線上,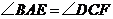 .
.
(1)求證: ;
;
(2)連結(jié)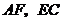 ,試猜想四邊形
,試猜想四邊形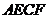 是什么四邊形,并證明你的結(jié)論.
是什么四邊形,并證明你的結(jié)論.
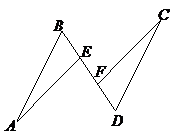 |
22.(本題滿分8分)
在一次投籃比賽中,甲、乙兩人共進行五輪比賽,每輪各投10個球,他們每輪投中的球數(shù)如下表:
輪次
一
二
三
四
五
甲投中(個)
6
8
7
5
9
乙投中(個)
7
8
6
7
7
(1)甲在五輪比賽中投中球數(shù)的平均數(shù)是 ,方差是 ;
(2)乙在五輪比賽中投中球數(shù)的平均數(shù)是 ,方差是 ;
(3)通過以上計算,你認為在比賽中甲、乙兩人誰的發(fā)揮更穩(wěn)定些?
23.(本題滿分9分)
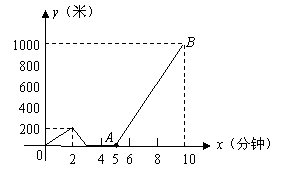
小文家與學(xué)校相距1000米.某天小文上學(xué)時忘了帶一本書,走了一段時間才想起,于是返回家拿書,然后加快速度趕到學(xué)校.下圖是小文與家的距離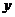 (米)關(guān)于時間
(米)關(guān)于時間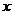 (分鐘)的函數(shù)圖象.請你根據(jù)圖象中給出的信息,解答下列問題:
(分鐘)的函數(shù)圖象.請你根據(jù)圖象中給出的信息,解答下列問題:
(1)小文走了多遠才返回家拿書?
(2)求線段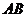 所在直線的函數(shù)解析式;
所在直線的函數(shù)解析式;
 (3)當(dāng)
(3)當(dāng)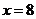 分鐘時,求小文與家的距離.
分鐘時,求小文與家的距離.
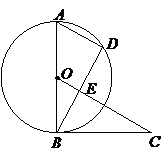
24.(本題滿分10分)
如圖所示,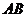 是
是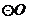 的直徑,
的直徑,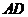 是弦,
是弦,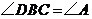 .
.
(1)求證: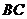 與
與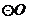 相切;
相切;
(2)若 ,
, 交
交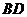 于點
于點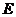 ,
,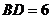 ,
,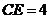 ,求
,求 的長.
的長.
 |
25.(本題滿分10分)
如圖所示,在一筆直的公路 的同一旁有兩個新開發(fā)區(qū)
的同一旁有兩個新開發(fā)區(qū) ,已知
,已知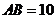 千米,直線
千米,直線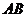 與公路
與公路 的夾角
的夾角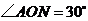 ,新開發(fā)區(qū)
,新開發(fā)區(qū)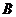 到公路
到公路 的距離
的距離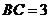 千米.
千米.
(1)求新開發(fā)區(qū) 到公路
到公路 的距離;
的距離;
(2)現(xiàn)要在 上某點
上某點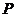 處向新開發(fā)區(qū)
處向新開發(fā)區(qū)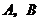 修兩條公路
修兩條公路 ,使點
,使點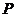 到新開發(fā)區(qū)
到新開發(fā)區(qū)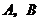 的距離之和最短.請你用尺規(guī)作圖在圖中找出點
的距離之和最短.請你用尺規(guī)作圖在圖中找出點 的位置(不用證明,不寫作法,保留作圖痕跡),并求出此時
的位置(不用證明,不寫作法,保留作圖痕跡),并求出此時 的值.
的值.
 |
26.(本題滿分12分)
如圖,已知拋物線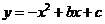 與
與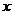 軸的兩個交點分別為
軸的兩個交點分別為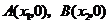 ,且
,且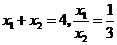 .
.
(1)分別求出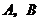 兩點的坐標(biāo);
兩點的坐標(biāo);
(2)求此拋物線的函數(shù)解析式;
(3)設(shè)此拋物線與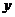 軸的交點為
軸的交點為 ,過
,過 作直線
作直線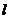 與拋物線交于另一點
與拋物線交于另一點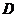 (點
(點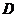 在
在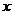 軸上方),連結(jié)
軸上方),連結(jié)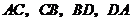 ,當(dāng)四邊形
,當(dāng)四邊形 的面積為4時,求點
的面積為4時,求點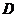 的坐標(biāo)和直線
的坐標(biāo)和直線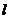 的函數(shù)解析式.
的函數(shù)解析式.
 |
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com