
2008屆江蘇省宿遷市初中畢業暨升學考試
數學試卷
答題注意事項
1. 答案全部寫在答題卡,寫在本試卷上無效。
2. 答選擇題時使用2B鉛筆,把答題卡上對應題號的選項字母涂滿、涂黑。如需修改,要用繪圖橡皮輕擦干凈再選涂其他選項。
3.
答非選擇題使用 黑色簽字筆,在答題卡上對應題號的答題區域書寫答案。注意不要答錯位置,也不要超界。
黑色簽字筆,在答題卡上對應題號的答題區域書寫答案。注意不要答錯位置,也不要超界。
一、選擇題(本大題共8小題,每小題3分,共24分,每題的四個選項中,只有一個符合題意):
1.下列計算正確的是
A.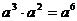 B.
B.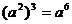
C.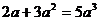 D.
D.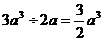
2.某市2008年第一季度財政收入為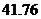 億元,用科學記數法(結果保留兩個有效數字)表示為
億元,用科學記數法(結果保留兩個有效數字)表示為
A. 元 B.
元 B.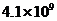 元 C.
元 C.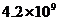 元 D.
元 D. 元
元
3.有一實物如圖,那么它的主視圖是

4.下列事件是確定事件的是
A.
C.2008年2月有29天 D.經過某一有交通信號燈的路口,遇到紅燈
5.下列圖形中既是軸對稱圖形又是中心對稱圖形的是
A.正六邊形 B.正五邊形 C.平行四邊形 D.等腰三角形
6.已知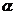 為銳角,且
為銳角,且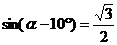 ,則
,則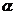 等于
等于
A.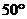 B.
B. C.
C.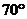 D.
D.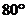
7.在平面直角坐標系中,函數 與
與 的圖象大致是
的圖象大致是

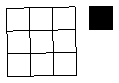
8.用邊長為 的正方形覆蓋
的正方形覆蓋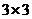 的正方形網格,最多覆蓋邊長為
的正方形網格,最多覆蓋邊長為 的正方形網格(覆蓋一部分就算覆蓋)的個數是
的正方形網格(覆蓋一部分就算覆蓋)的個數是
A. B.
B.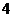 C.
C. D.
D.
二、填空題(本大題共10小題,每小題4分,共40分,請把答案直接填寫在答題卡相應位置上):
9.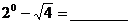 .
.
10.“兩直線平行,內錯角相等”的逆命題是__________.
11.因式分解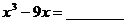 .
.
12.等腰三角形的兩邊長分別是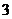 和
和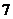 ,則其周長為______.
,則其周長為______.
13.若 有意義,則
有意義,則 的取值范圍是_________.
的取值范圍是_________.
14.若一個正多邊形的內角和是其外角和的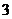 倍,則這個多邊形的邊數是______.
倍,則這個多邊形的邊數是______.
15.已知直角三角形兩條直角邊的長是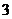 和
和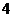 ,則其內切圓的半徑是______.
,則其內切圓的半徑是______.
16.已知一元二次方程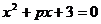 的一個根為
的一個根為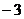 ,則
,則 .
.
17.用圓心角為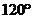 ,半徑為
,半徑為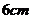 的扇形做成一個無底的圓錐側面,則此圓錐的底面半徑為
的扇形做成一個無底的圓錐側面,則此圓錐的底面半徑為 .
.
18.對于任意的兩個實數對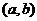 和
和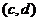 ,規定:當
,規定:當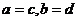 時,有
時,有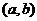
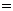
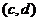 ;運算“
;運算“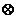 ”為:
”為: ;運算“
;運算“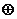 ”為:
”為: .設
.設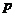 、
、 都是實數,若
都是實數,若 ,則
,則 .
.
三、解答題(本大題共9小題,滿分86分,請在答題卡指定區域內作答,解答應寫出必要的計算過程、推演步驟或文字說明):
19.(本題滿分8分)
解方程組: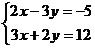
20.(本題滿分8分)
先化簡,再求值: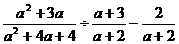 ,其中
,其中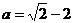 .
.
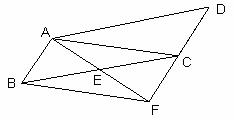
21.(本題滿分8分)
如圖,在平行四邊形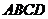 中,
中, 為
為 的中點,連接
的中點,連接 并延長交
并延長交 的延長線于點
的延長線于點 .
.
(1)求證: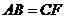 ;
;
(2)當 與
與 滿足什么數量關系時,
滿足什么數量關系時,
四邊形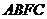 是矩形,并說明理由.
是矩形,并說明理由.
22.(本題滿分8分)
紅星中學團委為汶川地震災區組織獻愛心捐獻活動,小明對本班同學的捐款情況進行了統計,其中捐 元的人數占全班總人數的
元的人數占全班總人數的 .小明還繪制了頻數分布直方圖.
.小明還繪制了頻數分布直方圖.

(1)請求出小明所在班級同學的人數;
(2)本次捐款的中位數是____元;
(3)請補齊頻數分布直方圖.
23.(本題滿分10分)
如圖,⊙ 的直徑
的直徑 是
是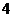 ,過
,過 點的直線
點的直線 是⊙
是⊙ 的切線,
的切線, 、
、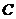 是⊙
是⊙ 上的兩點,連接
上的兩點,連接 、
、 、
、 和
和 .
.

(1)求證: ;
;
(2)若 是
是 的平分線,且
的平分線,且 ,求
,求 的長.
的長.
24.(本題滿分10分)
如圖,已知反比例函數 的圖象與一次函數
的圖象與一次函數 的圖象交于
的圖象交于 、
、 兩點,
兩點, .
.
(1)求反比例函數和一次函數的關系式;
(2)在直線 上是否存在一點
上是否存在一點 ,使
,使 ∽
∽ ,若存在,求
,若存在,求 點坐標;若不存在,請說明理由.
點坐標;若不存在,請說明理由.

25.(本題滿分11分)
不透明的口袋里裝有紅、黃、藍三種顏色的小球(除顏色外其余都相同),其中紅球有 個,藍球有
個,藍球有 個,現從中任意摸出一個是紅球的概率為
個,現從中任意摸出一個是紅球的概率為 .
.
(1)求袋中黃球的個數;
(2)第一次摸出一個球(不放回),第二次再摸一個小球,請用畫樹狀圖或列表法求兩次摸到都是紅球的概率;
(3)若規定摸到紅球得 分,摸到黃球得
分,摸到黃球得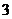 分,摸到藍球得
分,摸到藍球得 分,小明共摸
分,小明共摸 次小球(每次摸
次小球(每次摸 個球,摸后放回)得
個球,摸后放回)得 分,問小明有哪幾種摸法?
分,問小明有哪幾種摸法?
26.(本題滿分11分)
某賓館有客房 間,當每間客房的定價為每天
間,當每間客房的定價為每天 元時,客房會全部住滿.當每間客房每天的定價每漲
元時,客房會全部住滿.當每間客房每天的定價每漲 元時,就會有
元時,就會有 間客房空閑.如果旅客居住客房,賓館需對每間客房每天支出
間客房空閑.如果旅客居住客房,賓館需對每間客房每天支出 元的各種費用.
元的各種費用.
(1)請寫出該賓館每天的利潤 (元)與每間客房漲價
(元)與每間客房漲價 (元)之間的函數關系式;
(元)之間的函數關系式;
(2)設某天的利潤為 元,
元, 元的利潤是否為該天的最大利潤?如果是,請說明理由;如果不是,請求出最大利潤,并指出此時客房定價應為多少元?
元的利潤是否為該天的最大利潤?如果是,請說明理由;如果不是,請求出最大利潤,并指出此時客房定價應為多少元?
(3)請回答客房定價在什么范圍內賓館就可獲得利潤?
27.(本題滿分12分)
如圖,⊙ 的半徑為
的半徑為 ,正方形
,正方形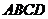 頂點
頂點 坐標為
坐標為 ,頂點
,頂點 在⊙
在⊙ 上運動.
上運動.
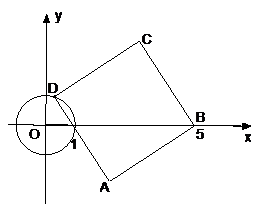
(1)當點 運動到與點
運動到與點 、
、 在同一條直線上時,試證明直線
在同一條直線上時,試證明直線 與⊙
與⊙ 相切;
相切;
(2)當直線 與⊙
與⊙ 相切時,求
相切時,求 所在直線對應的函數關系式;
所在直線對應的函數關系式;
(3)設點 的橫坐標為
的橫坐標為 ,正方形
,正方形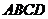 的面積為
的面積為 ,求
,求 與
與 之間的函數關系式,并求出
之間的函數關系式,并求出 的最大值與最小值.
的最大值與最小值.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com