
2008-2009學年度濰坊市奎文區第一學期九年級期中考試
數學試卷
時間:120分鐘 120分
一、選擇題(共10個小題,每小題3分,共30分)
1.下列關于 的方程中,一定是一元二次方程的是( )
的方程中,一定是一元二次方程的是( )
A.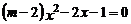 B.
B.
C.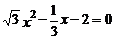 D.
D.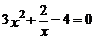
2.下列二次根式中,與 是同類二次根式的是( )
是同類二次根式的是( )
A.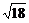 B.
B.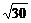 C.
C.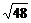 D.
D.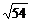
3.用配方法解方程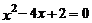 ,下列配方正確的是( )
,下列配方正確的是( )
A.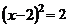 B.
B.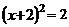 C.
C.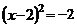 D.
D.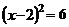
4.下列關于 的一元二次方程中,有兩個不相等的實數根的方程是( ).
的一元二次方程中,有兩個不相等的實數根的方程是( ).
A.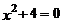 B.
B.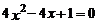
C.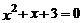 D.
D.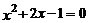
5.將拋物線 向上平移2個單位,得到拋物線的解析式是( ).
向上平移2個單位,得到拋物線的解析式是( ).
A.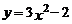 B.
B. C.
C.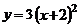 D.
D.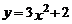
6.若 ,則
,則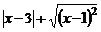 的值為( ).
的值為( ).
A.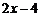 B.
B.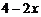 D.2
D.2
7.若拋物線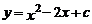 與
與 軸的交點為(0,-3),則下列說法不正確的是( )
軸的交點為(0,-3),則下列說法不正確的是( )
A.拋物線開口向上
B.拋物線的對稱軸是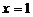
C.當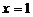 時,
時, 的最大值為-4
的最大值為-4
D.拋物線與 軸的交點為(-1,0),(3,0)
軸的交點為(-1,0),(3,0)
8.煙花廠設計制作了一種新型禮炮,這種禮炮的升空高度 (m)與飛行時間
(m)與飛行時間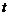 (s)的關系式是
(s)的關系式是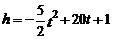 ,若這種禮炮在點火升空到最高點處引爆,則從點火升空到引爆需要的時間為( ).
,若這種禮炮在點火升空到最高點處引爆,則從點火升空到引爆需要的時間為( ).
A.3s B.4s C.5s D.6s
9.拋物線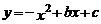 的部分圖象如圖所示,若
的部分圖象如圖所示,若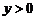 ,則
,則 的取值范圍是( ).
的取值范圍是( ).
A.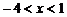 B.
B.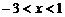 C.
C.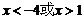 D.
D.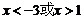

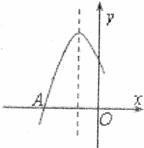
10.如下圖是二次函數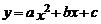 圖象的一部分,圖象過點A(-3,0),對稱軸為
圖象的一部分,圖象過點A(-3,0),對稱軸為 .給出四個結論:①
.給出四個結論:①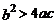 ;②
;②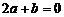 ;③
;③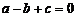 ;④
;④ .其中正確結論是( ).
.其中正確結論是( ).
A.②④ B.①④ C.②③ D.①③
二、填空題(共10個小題,每小題3分,共30分)
11.當 __________時,二次根式
__________時,二次根式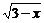 有意義.
有意義.
12.化簡: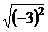 =__________.
=__________.
13.關于 的一元二次方程
的一元二次方程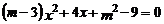 有一個根為0,
有一個根為0, 的值為__________.
的值為__________.
14.拋物線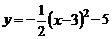 的對稱軸是__________.
的對稱軸是__________.
15.關于 的一元二次方程
的一元二次方程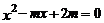 的一個根為1,則方程的另一根為__________.
的一個根為1,則方程的另一根為__________.
16.一元二次方程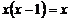 的解是__________.
的解是__________.
17.如下圖所示的拋物線是二次函數 的圖象,那么
的圖象,那么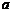 的值是__________.
的值是__________.
18.拋物線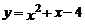 與
與 軸的交點坐標為__________.
軸的交點坐標為__________.
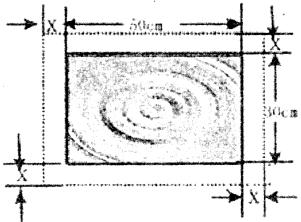
19.如圖,在一幅長50 ,寬30
,寬30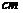 的風景畫的四周鑲一條金色紙邊,制成一幅矩形掛圖,如果要使整個矩形掛圖的面積是1800
的風景畫的四周鑲一條金色紙邊,制成一幅矩形掛圖,如果要使整個矩形掛圖的面積是1800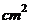 ,設金色紙邊的寬為
,設金色紙邊的寬為
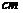 ,那么
,那么 滿足的方程為__________.
滿足的方程為__________.
20.如下圖,小明的父親在相距2米的兩棵樹間拴了一根繩子,給他做了一個簡易的秋千,拴繩子的地方距地面高都是2.5米,繩子自然下垂呈拋物線狀,身高1米的小明距較近的那棵樹0.5米時,頭部剛好接觸到繩子,則繩子的最低點距地面的距離為__________米.

三、解答題(本題8個小題,共60分)
21.計算:(每小題3分,共6分)
(1)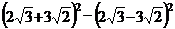
(2)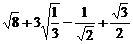
22.解方程:(每小題3分,共6分)
(1)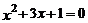
(2)用配方法解方程: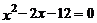
23.(6分)已知關于 的一元二次方程
的一元二次方程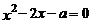 .
.
(1)如果此方程有兩個不相等的實數根,求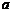 的取值范圍;
的取值范圍;
(2)如果此方程的兩個實數根為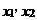 ,且滿足
,且滿足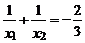 ,求
,求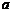 的值.
的值.
24.(8分)已知拋物線與 軸的交點是A(-2,0)、B(1,0),且經過點C(2,8)
.
軸的交點是A(-2,0)、B(1,0),且經過點C(2,8)
.
(1)求該拋物線的解析式;
(2)求該拋物線的頂點坐標.
25.(8分)汽車產業的發展,有效促進我國現代化建設.某汽車銷售公司2005年盈利1500萬元,到2007年盈利2160萬元,且從2005年到2007年,每年盈利的年增長率相同.
(1)該公司2006年盈利多少萬元?(6分)
(2)若該公司盈利的年增長率繼續保持不變,預計2008年盈利多少萬元?(2分)
26.(8分)為了改善小區環境,某小區決定要在一塊一邊靠墻(墻長25 )的空地上修建一個矩形綠化帶ABCD,綠化帶一邊靠墻,另三邊用總長為40
)的空地上修建一個矩形綠化帶ABCD,綠化帶一邊靠墻,另三邊用總長為40 的柵欄圍住(如下圖).若設綠化帶的BC邊長為
的柵欄圍住(如下圖).若設綠化帶的BC邊長為
 ,綠化帶的面積為
,綠化帶的面積為
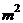 .
.
(1)求 與
與 之間的函數關系式,并寫出自變量
之間的函數關系式,并寫出自變量 的取值范圍;
的取值范圍;
(2)當 為何值時,滿足條件的綠化帶的面積最大?
為何值時,滿足條件的綠化帶的面積最大?
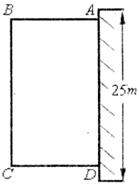
27.(9分)如圖,隧道的截面由拋物線AED和矩形ABCD構成,矩形的長BC為8 ,寬AB為2
,寬AB為2 ,以BC所在的直線為
,以BC所在的直線為 軸,線段BC的中垂線為
軸,線段BC的中垂線為 軸,建立平面直角坐標系,
軸,建立平面直角坐標系, 軸是拋物線的對稱軸,頂點E到坐標原點O的距離為6
軸是拋物線的對稱軸,頂點E到坐標原點O的距離為6 .
.
(1)求拋物線的解析式;
(2)一輛貨運卡車高4.5 ,寬2.4
,寬2.4 ,它能通過該隧道嗎?
,它能通過該隧道嗎?
(3)如果該隧道內設雙行道,為了安全起見,在隧道正中間設有0.4 的隔離帶,則該輛貨運卡車還能通過隧道嗎?
的隔離帶,則該輛貨運卡車還能通過隧道嗎?

28.(9分)某水果批發商銷售每箱進價為40元的蘋果,物價部門規定每箱售價不得高于55元,市場調查發現,若每箱以50元的價格售出,平均每天銷售90箱,價格每提高1元,平均每天少銷售3箱.
(1)求平均每天銷售最 (箱)與銷售價
(箱)與銷售價 (元/箱)之間的函數關系式.
(元/箱)之間的函數關系式.
(2)求該批發商平均每天的銷售利潤 (元)與銷售價
(元)與銷售價 (元/箱)之間的函數關系式.
(元/箱)之間的函數關系式.
(3)當每箱蘋果的銷售價為多少元時,可以獲得最大利潤?最大利潤是多少?
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com