
2008-2009學年度招遠市第二學期初三第二學段測評
數學試題
說明:本試卷試題115分,書寫質量3分,卷面安排2分,滿分120分;考試時間120分鐘。
一、選擇題(每小題2分,滿分30分)
1.下列函數中,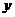 是
是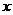 的反比例函數的是
的反比例函數的是
A.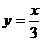 B.
B.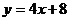 C.
C.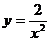 D.
D.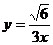
2.下列命題中,真命題是
A.兩條對角線互相垂直的四邊形是菱形
B.對角線互相垂直且相等的四邊形是正方形
C.兩條對角線相等的四邊形是矩形
D.兩條對角線相等的平行四邊形是矩形
3.有4條線段,長度分別為
A.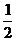 B.
B. C.
C.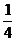 D.
D.
4.一元二次方程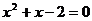 的根的情況是
的根的情況是
A.有兩個不相等的實數根 B.無實數根
C.有兩個相等的實數根 D.無法確定
5.下列函數中,圖像經過點(1,-1)的反比例函數表達式是
A.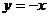 B.
B.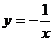 C.
C.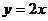 D.
D.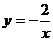
6.△ABC的面積為
A.
7.第十一屆全國運動會將于
A.60張 B.80張 C.90張 D.100張
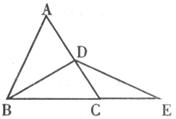
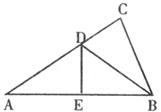
8.如下圖,D為等邊△ABC的AC邊的中點,E為BC延長線上一點,且DB=DE,若△ABC的周長為12,則△DCE的周長為
A.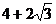 B.
B.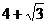 C.
C. 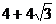 D.4
D.4
9.一次函數 和反比例函數
和反比例函數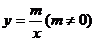 在同一坐標系中的圖像大致是
在同一坐標系中的圖像大致是
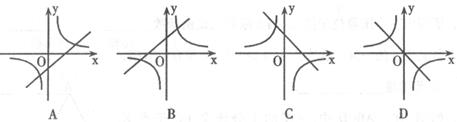
10.菱形的一條對角線長是
A.
11.等腰三角形的底和腰是方程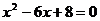 的兩根,則這個三角形的周長為
的兩根,則這個三角形的周長為
A.10 B.
12.用數字1,2,3隨機排成一個三位數,得到奇數的概率是
A.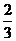 B.
B.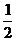 C.
C. D.
D.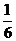
13.如下圖,AD是直角△ABC的斜邊BC上的高,BE平分∠ABC,交AD于E,EF∥AC,交DC于F。則下列結論中―定成立的是
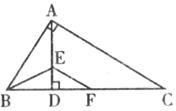
A.∠ABE=∠DFE B.AE=ED C.AD=DC D.AB=BF
14.函數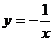 的圖像上有兩點A(
的圖像上有兩點A(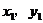 )、B(
)、B(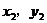 ),且
),且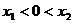 ,那么下列結論正確的是
,那么下列結論正確的是
A.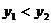 B.
B.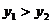
C.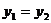 D.
D.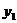 與
與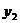 的大小關系不確定
的大小關系不確定
15.如下圖,EF是梯形ABCD的中位線,則△AEF的面積與梯形ABCD的面積之比為

A.1:3 B.1:4 C.1:5 D.1:6
16.請寫出一個圖像位于第二、四象限的反比例函數__________。
17.若關于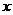 的一元二次方程
的一元二次方程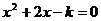 沒有實數根,則
沒有實數根,則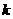 的取值范圍是__________。
的取值范圍是__________。
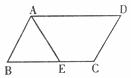
18.如下圖,在□ABCD中,∠A的平分線交BC于點E,若AB=
19.某射手在相同條件下進行射擊訓練,結果如下表所示:
射擊次數
10
20
50
100
200
500
擊中靶心次數
9
19
44
91
178
450
擊中靶心頻率
0.90
0.95
0.88
0.91
0.89
0.90
試根據該表,估計這名射手射擊一次,擊中靶心的概率約為__________。
20.如下圖,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠EAB,則∠ACD的度數為_________。
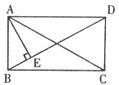
21.如下圖,在△ABC中,AB=AC,DE是線段AB的垂直平分線,交AC于點D,交AB于點E,若∠C=70°,則∠DBC=__________度。
22.若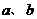 是方程
是方程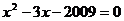 的兩個根,則代數式
的兩個根,則代數式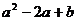 的值為__________。
的值為__________。
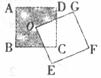
23.如下圖,正方形ABCD和正方形OEFG的邊長均為4,O為正方形ABCD的中心,則圖中陰影部分的面積是__________。
24.兩個裝有乒乓球的盒子,其中一個裝有2個白球,1個黃球;另一個裝有1個白球,2個黃球。現從這兩個盒中隨機各抽取一個球,則取出的兩個球一個是白球一個是黃球的概率是__________。
25.已知點A是函數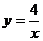 的圖像上的一點,AB
的圖像上的一點,AB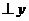 軸于點B,O為原點,則△AOB面積是__________。
軸于點B,O為原點,則△AOB面積是__________。
三、解答題(每小題8分,滿分24分)
26.解方程: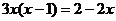
27.若函數 是反比例函數,且它的圖像位于第一、三象限內,求
是反比例函數,且它的圖像位于第一、三象限內,求 的值。
的值。
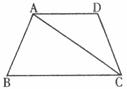
28.如下圖,在等腰梯形ABCD中,AB=CD,∠D=120°,AC平分∠BCD,梯形的中位線長為6,求AC的長及梯形的面積。
四、實際應用題(每小題10分,滿分20分)
29.袋中裝有質地、大小相同的紅球、藍球、白球各一個,搖勻后從中摸出一個球,然后放回,搖勻后再摸出一個球。
(1)請你用列表的方法或畫樹狀圈的方法分析兩次摸出的球的所有結果;
(2)求出兩次摸出顏色相同的球的概率。
30.為預防“甲型H1N1流感”,某校對教室進行“藥熏消毒”。已知藥物燃燒階段,室內每立方米空氣中的含藥量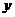 (毫克)與燃燒時間
(毫克)與燃燒時間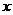 (分鐘)成正比例;燃燒結束后,
(分鐘)成正比例;燃燒結束后,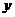 與
與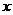 成反比例(如下圖所示),現測得藥物10分鐘燃燒完,此時教室內每立方米空氣中含藥量為8毫克。
成反比例(如下圖所示),現測得藥物10分鐘燃燒完,此時教室內每立方米空氣中含藥量為8毫克。
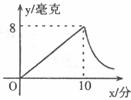
請根據以上信息解答下列問題:
(1)求藥物燃燒時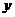 與
與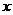 的函數表達式;
的函數表達式;
(2)求藥物燃燒結束后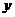 與
與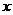 的函數表達式;
的函數表達式;
(3)如果當每立方米空氣中含藥量低于1.6毫克時,才能對人體無毒害作用,那么從消毒開始,經多長時間學生才可以回教室?
五、探索題(滿分11分)
31.如下圖,在□ABCD中,AB⊥AC,對角線BD,AC相交于點O,將直線AC繞著點O順時針旋轉,分別交BE,AD于點E、F。
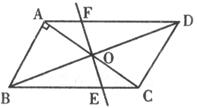
(1)證明:當旋轉角為90°時,四邊形ABEF是平行四邊形;
(2)請你探索在旋轉過程中,線段AF與CE的數量關系,并給出證明;
(3)若AB=1,BC=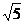 ,在旋轉過程中,四邊形BEDF可能是菱形嗎?如果不能,請說明理由;如果能,說明理由并求此時AC繞點O順時針旋轉的度數。
,在旋轉過程中,四邊形BEDF可能是菱形嗎?如果不能,請說明理由;如果能,說明理由并求此時AC繞點O順時針旋轉的度數。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com