
內(nèi)蒙古海拉爾二中2009屆高三第六次階段考試
理科數(shù)學(xué) (2009.5.15)
時間:120分鐘 分值:150分
第Ⅰ卷(選擇題 共60分)
一.選擇題:本大題共12小題,每小題5分,共60分.在每小題給出的四個選項中,只有一項是符合題目要求的.
1.設(shè)集合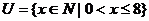 ,
,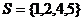 ,
,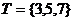 ,則
,則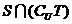 =
=
 .
.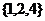
 .
.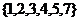
 .
.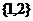
 .
.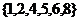
2. 已知復(fù)數(shù)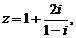 則
則 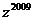 的值為
的值為
 .
.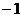
 .
.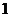
 .
.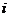
 .
.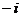
3.正項數(shù)列{an}成等比數(shù)列,a1+a2=3,a3+a4=12,則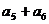 的值是
的值是
 . -24
. -24
 . 21
. 21
 . 24
. 24  . 48
. 48
4.函數(shù)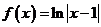 的圖像大致形狀是
的圖像大致形狀是
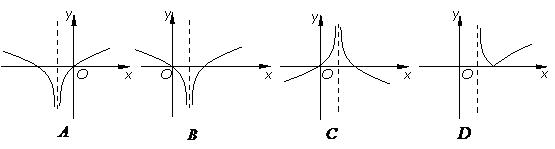 |
5.在四邊形ABCD中,“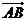 =
=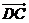 ”是“四邊形ABCD為梯形”的
”是“四邊形ABCD為梯形”的
 .充分不必要條件
.充分不必要條件  .必要不充分條件
.必要不充分條件  .充要條件
.充要條件  .既不充分也不必要條件
.既不充分也不必要條件
6某校根據(jù)新課程標(biāo)準(zhǔn)改革的要求,開設(shè)數(shù)學(xué)選修4系列的10門課程供學(xué)生選修,其中4―1,4―2,4―4三門由于上課時間相同,所以至多選一門,根據(jù)學(xué)分制要求,每位同學(xué)必須選修三門,則每位同學(xué)不同的選修方案種數(shù)是
 .
.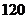 ;
;  .
.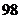 ;
;  .
.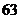 ;
;  .
.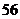 ;
;
7.一個正方體的頂點都在球面上,它的棱長為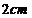 ,則球的表面積是
,則球的表面積是
 .
.
 .
.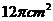
 .
.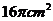
 .
.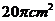
8.已知函數(shù)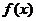 是定義在
是定義在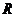 上的奇函數(shù),當(dāng)
上的奇函數(shù),當(dāng)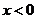 時,
時,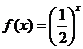 ,那么
,那么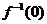 的值為
的值為
 .
.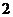
 .
.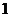
 .
.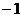
 .
.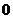
9. 已知拋物線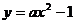 的焦點是坐標(biāo)原點,則以拋物線與兩坐標(biāo)軸的三個交點為頂點的三角形面積為
的焦點是坐標(biāo)原點,則以拋物線與兩坐標(biāo)軸的三個交點為頂點的三角形面積為
 .
.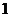
 .
.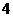
 .
.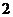
 .
.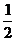
10.已知正三棱錐的側(cè)棱長是底面邊長的2倍,則側(cè)棱與底面所成角的余弦值等于
 .
.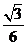
 .
.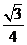
 .
.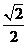
 .
.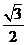
11. 在二項式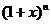 的展開式中,存在系數(shù)之比為
的展開式中,存在系數(shù)之比為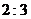 的相鄰兩項,則指數(shù)
的相鄰兩項,則指數(shù)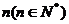 的最小值為
的最小值為
 .6
.6  .5
.5  .4
.4  .3
.3
12.雙曲線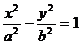
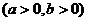 的兩個焦點為
的兩個焦點為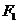 、
、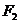 ,若
,若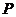 為其上一點,且
為其上一點,且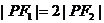 ,則雙曲線離心率的取值范圍為
,則雙曲線離心率的取值范圍為
 .
.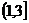
 .
.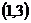
 .
.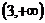
 .
.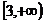
海拉爾二中2009屆高三第六次階段考試試題(理)
第Ⅱ卷(非選擇題,共90分)
二、填空題(本大題共4小題,每小題5分,共20分,把答案填在題中的橫線上)
13. 實數(shù)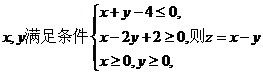 的最大值為________ .
的最大值為________ .
14. 設(shè)曲線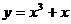 在點
在點 處的切線與直線
處的切線與直線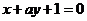 垂直,則
垂直,則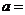 ______.
______.
15. 將圓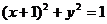 按向量
按向量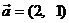 平移后,恰好與直線
平移后,恰好與直線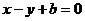 相切,則
相切,則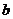 =_______
=_______
16. 在某項測量中,測量結(jié)果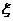 服從正態(tài)分布
服從正態(tài)分布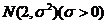 ,若
,若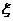 在(0,2)內(nèi)
在(0,2)內(nèi)
取值的概率為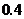 ,則
,則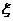 在
在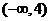 內(nèi)取值的概率為_______
內(nèi)取值的概率為_______
三.解答題(本大題共6小題,解答應(yīng)寫出文字說明.證明過程或演算步驟)
17.(本小題滿分10分)已知向量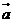 =(sin(
=(sin(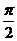 +x),
+x),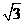 cosx),
cosx),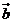 =(sinx, cosx), f(x)=
=(sinx, cosx), f(x)= 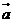 ?
?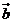 .
.
⑴求f(x)的最小正周期和單調(diào)增區(qū)間;
⑵如果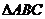 中,滿足
中,滿足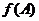 =
=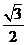 ,求角A的值.
,求角A的值.
18.(本小題滿分12分) 某次抽獎活動,有彩票號從0001到1000共1000張彩票,其中彩票號為0123是一等獎,獎金5000元;彩票號后兩位數(shù)為23的是二等獎,獎金1000元;彩票號尾數(shù)為3是三等獎,獎金20元.
(1)某人買了2張彩票,問他獲得一等獎或二等獎的概率是多少?(用分?jǐn)?shù)表示)
(2)某人買了1張彩票,求他獲得獎金數(shù)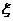 的分布列以及期望
的分布列以及期望
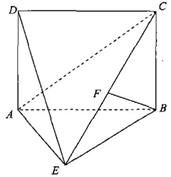 19.(本小題滿分12分) 如圖,直二面角
19.(本小題滿分12分) 如圖,直二面角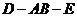 ,四邊形
,四邊形 是邊長為2的正方形,
是邊長為2的正方形,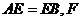 為CE上的點,且
為CE上的點,且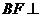 平面
平面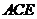 .
.
(1)求證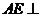 平面
平面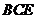 ;
;
(2)求二面角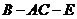 的大小.
的大小.
20.(本小題滿分12分) 設(shè)數(shù)列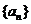 滿足:
滿足:
(1)令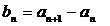 ,求數(shù)列
,求數(shù)列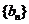 的通項公式;
的通項公式;
(2)求數(shù)列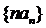 的前
的前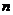 項和
項和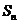 .
. 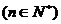
21.(本題12分)橢圓 的中心為坐標(biāo)原點,焦點在
的中心為坐標(biāo)原點,焦點在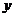 軸上,焦點到相應(yīng)準(zhǔn)線的距離及離心率均為
軸上,焦點到相應(yīng)準(zhǔn)線的距離及離心率均為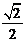 ,直線
,直線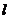 與
與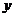 軸交于點
軸交于點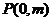 ,與橢圓
,與橢圓 交于相異兩點
交于相異兩點 ,
,
(1)求橢圓方程;
(2)若 ,求
,求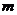 的取值范圍.
的取值范圍.
22.(本題滿分12分) 已知函數(shù)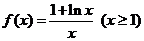
(1)試判斷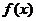 的單調(diào)性,并說明理由;
的單調(diào)性,并說明理由;
(2)若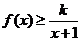 恒成立,求實數(shù)
恒成立,求實數(shù)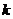 的取值范圍;
的取值范圍;
一.選擇題:



 二、填空題: 13.
二、填空題: 13.  14.
14.  15.
15.  16.
16. 
三.解答題
17.解:⑴f(x)= sinxcosx+ +
+ cos2x =
sin(2x+
cos2x =
sin(2x+ )+
)+
T=π,2 kπ- ≤2x+
≤2x+ ≤2 kπ+
≤2 kπ+ ,k∈Z,
,k∈Z,
最小正周期為π,單調(diào)增區(qū)間[kπ- ,kπ+
,kπ+ ],k∈Z.
],k∈Z.
⑵由sin(2A+ )=0,
)=0, <2A+
<2A+ <
< ,
,
∴2A+ =π或2π,∴A=
=π或2π,∴A= 或
或
18. 解:(1)
(2)設(shè)各等獎的獎金數(shù)為ξ則
ξ
5000
1000
20
0
P
0.001
0.009
0.09
0.9
∴Eξ=5+9+1.8+0=15.8(元)
19.解:(1) 平面
平面
∵二面角 為直二面角,且
為直二面角,且 ,
,
 平面
平面
 平面
平面 .
.
(2)連接 與高
與高 交于
交于 ,連接
,連接 是邊長為2的正方形,
是邊長為2的正方形,  ,
,
 二平面
二平面 ,由三垂線定理逆定理得
,由三垂線定理逆定理得
 是二面角
是二面角 的平面角
的平面角
由(1) 平面
平面 ,
,
 .
.
在 中,
中,
∴在 中,
中,
故二面角 等于
等于 .
.
(2)可用向量法
20. 解:(1)因
故 是公比為
是公比為 的等比數(shù)列,且
的等比數(shù)列,且
故 .
.
(2)由 得
得



注意到 ,可得
,可得 ,即
,即
記數(shù)列 的前
的前 項和為
項和為 ,則
,則
 兩式相減得:
兩式相減得:

故
從而
 .
.
21.解:(1)由 得
得
∴橢圓 的方程為:
的方程為: .
.
(2)設(shè)直線 的方程為:
的方程為:
由 得
得


由此得 . ①
. ①
設(shè) 與橢圓
與橢圓 的交點為
的交點為 ,則
,則
由 得
得
 ,整理得
,整理得
 ,整理得
,整理得
 時,上式不成立,
時,上式不成立, ②
②
由式①、②得
 或
或
∴ 取值范圍是
取值范圍是 .
.
22.,解(1)
 故
故 在
在 遞減
遞減
(2) 記
記

再令 
 在
在 上遞增
上遞增
 ,從而
,從而  故
故 在
在 上也單調(diào)遞增
上也單調(diào)遞增

國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com