
假期復習第十四天―――不等式
一.這幾個概念你掌握了嗎?請回顧一遍:
1. 不等式的基本性質有哪些?
2.均值不等式及其它幾個重要不等式是否很熟練;
3.如何用分析法、綜合法、比較法等證明簡單的不等式;
4.分式不等式、二次不等式、對指數不等式、含絕對值不等式怎么解?
5.絕對值不等式的性質是什么,怎么樣理解?
二.特別要注意下列方法:
1.比較法是不等式證明中最基本、也是最常用的方法,比較法的一般步驟是:作差(商)→變形→判斷符號(值).
2.在解不等式中,換元法和圖解法是常用的技巧之一.通過換元,可將較復雜的不等式化歸為較簡單的或基本不等式,通過構造函數、數形結合,則可將不等式的解化歸為直觀、形象的圖形關系,對含有參數的不等式,運用圖解法可以使得分類標準明晰;
3.不等式應用問題體現了一定的綜合性.這類問題大致可以分為兩類:一類是建立不等式、解不等式;另一類是建立函數式求最大值或最小值.利用平均值不等式求函數的最值時,要特別注意“正數、定值和相等”三個條件缺一不可,有時需要適當拼湊,使之符合這三個條件.利用不等式解應用題的基本步驟:10審題,20建立不等式模型,30解數學問題,40作答。
三.下列習題你必須掌握:
1、不等式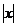 〉
〉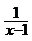 的解集是
的解集是
A.(-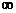 ,1)
B.(-
,1)
B.(-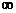 ,1)
,1)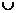 (1,
(1,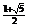 )
)
C.(-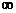 ,1)
,1)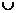 (
(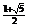 ,+
,+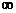 )
D.(-
)
D.(-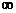 ,0)
,0)
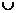 (
(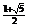 +
+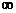 )
)
2、下列各組命題中,M是N的充要條件的是
A.M: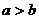 ;N:
;N: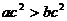 B.M:
B.M: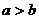 ,
,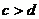 ;N:
;N: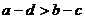
C.M: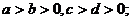 N:
N: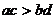 D.
D.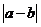 =
=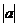 +
+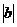 ;N:
;N: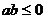
3、不等式組
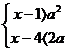 有解,則實數a的取值范圍是
有解,則實數a的取值范圍是
A.(-1,3)
B.(- ,-1)
,-1)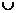 (3,+
(3,+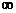 )
)
C.(-3,1)
D.(-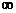 ,-3)
,-3)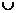 (1,+
(1,+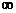 )
)
4、若 ,
,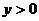 且
且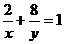 ,則
,則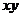 有
有
A.最大值64 B.最小值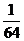 D.最小值
D.最小值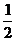
5、若不等式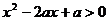 對
對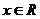 恒成立,則關于
恒成立,則關于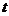 的不等式
的不等式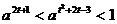 的解為
的解為
A.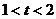 B.
B.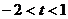 C.
C.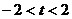 D.
D.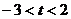
1. 不等式的基本性質有:
(1)對稱性:a>b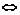 b<a;
b<a;
(2)傳遞性:若a>b,b>c,則a>c;
(3)可加性:a>b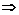 a+c>b+c,
a+c>b+c,
(4)可乘性:a>b,當c>0時,ac>bc;當c<0時,ac<bc。
2.不等式運算性質:
(1)同向相加:若a>b,c>d,則a+c>b+d;
(2)正數同向相乘:若a>b>0,c>d>0,則ac>bd。
(3)乘(開)方法則:若a>b>0,n∈N+,則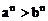 (
(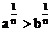 );
);
(4)倒數法則:若ab>0,a>b,則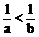 。
。
3.重要不等式
(1)a2+b2≥2ab(a,b∈R)
(2)當a,b≥0時,a+b≥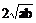
或ab≤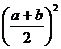
(3)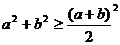
4.均值不等式的性質:
||a|-|b||≤|a+b|≤|a|+|b|
(1)ab≥0Û|a+b|=|a|+|b|
(2)ab<0Û|a+b|<|a|+|b|
(3)ab≤0Û|a+b|=||a|-|b||
(4)ab>0Û|a+b|>||a|-|b||
6、設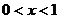 ,則函數
,則函數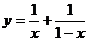 的最小值為 _____
的最小值為 _____
7、不等式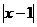 <
<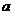 成立的充分條件是
成立的充分條件是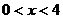 ,則
,則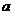 的取值范圍是______
的取值范圍是______
8、已知有向線段PQ的起點P和終點Q的坐標分別為(-1,1)和(2,2),直線L: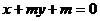 與PQ的延長線的相交,則
與PQ的延長線的相交,則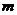 的取值范圍是 ____
的取值范圍是 ____
9.已知x≥0、y≥0,求證: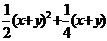 ≥
≥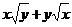
(請用多種方法做)
10.解關于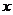 的不等式
的不等式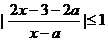
11.已知f(x)=-3x2+a(6-a)x+b
(1)解關于a的不等式f(1)>0;
(2)當不等式f(x)>0的解集為(-1,3)時,求實數a,b的值。
12.已知A、B兩地相距200千米,一只船從A地逆水到
B地,水速為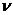 千米/
千米/
小時(8<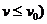 。若船每小時的燃料費與其在靜水中的
。若船每小時的燃料費與其在靜水中的
速度的平方成正比,當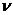 =
=
為720元,為了使全程燃油費最省,船的實際速度應為多
少?
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com