題目列表(包括答案和解析)
(本小題滿分12分)
如圖，在平面直角坐標系
中，△ABC的A、B兩個頂點在x軸上，頂點C在y軸的負半軸上．已知
，
，△ABC的面積
，拋物線
經過A、B、C三點。
1.(1)求此拋物線的函數表達式；
2.(2)設E是y軸右側拋物線上異于點B的一個動點，過點E作x軸的平行線交拋物線于另一點F，過點F作FG垂直于x軸于點G，再過點E作EH垂直于x軸于點H，得到矩形EFGH．則在點E的運動過程中，當矩形EFGH為正方形時，求出該正方形的邊長；
3.(3)在拋物線上是否存在異于B、C的點M，使△MBC中BC邊上的高為
？若存在，求出點M的坐標；若不存在，請說明理由．
(本小題滿分12分，每題6分)
(1)計算：
。
（2）解不等式組：
，并寫出該不等式組的最小整數解。
(本小題滿分12分)
1. (1)觀察發現
如(a)圖，若點A，B在直線
同側，在直線上找一點P，使AP+BP的值最小．
做法如下：作點B關于直線的對稱點
，連接
，與直線的交點就是所求的點P
再如(b)圖，在等邊三角形ABC中，AB=2，點E是AB的中點，AD是高，在AD上找一點P，使BP+PE的值最小．
做法如下：作點B關于AD的對稱點，恰好與點C重合，連接CE交AD于一點，則這點就是所求的點P，故BP+PE的最小值為 ． (2分)
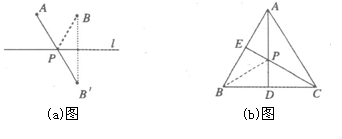
2.(2)實踐運用
如圖，菱形ABCD的兩條對角線分別長6和8，點P是對角線AC上的一個動點，點M、N分別是邊AB、BC的中點，求PM+PN的最小值。(5分)
3.(3)拓展延伸
如(d)圖，在四邊形ABCD的對角線AC上找一點P，使∠APB=∠APD．保留作圖痕跡，不必寫出作法． (5分)
(本小題滿分12分)
如圖，在平面直角坐標系xoy中，矩形ABCD的邊AB在x軸上，且AB=3，BC=
，直線y=
經過點C，交y軸于點G。
1.（1）點C、D的坐標分別是C（ ），D（ ）；
2.（2）求頂點在直線y=上且經過點C、D的拋物
線的解析式；
3.（3）將（2）中的拋物線沿直線y=平移，平移后
的拋物線交y軸于點F，頂點為點E（頂點在y軸右側）。
平移后是否存在這樣的拋物線，使⊿EFG為等腰三角形？
若存在，請求出此時拋物線的解析式；若不存在，請說
明理由。
(本小題滿分12分)
如圖，直角梯形ABCD中，AB∥DC，∠DAB=90°，AD=2DC=4，AB=6．動點M以每秒1個單位長的速度，從點A沿線段AB向點B運動；同時點P以相同的速度，從點C沿折線C-D-A向點A運動．當點M到達點B時，兩點同時停止運動．過點M作直線l∥AD，與折線A-C-B的交點為Q．點M運動的時間為t（秒）．
（1）當
時，求線段
的長；
（2）點M在線段AB上運動時，是否可以使得以C、P、Q為頂點的三角形為直角三角形，若可以，請直接寫出t的值（不需解題步驟）；若不可以，請說明理由．
（3）若△PCQ的面積為y，請求y關于出t 的函數關系式及自變量的取值范圍；
一、選擇題
1．A 2．B 3．C 4．D 5．C 6．A 7．D 8．C
二、填空題
9．－5 10．3 11．x＝1 12．2 13．105
三、解答題
14．解： 
= 1 + 2 + (－2) …………6分.
=1 …………7分.
15．解：由題意，得x－3>0，∴x>3， …………2分
∴原式=
…………4分
=
…………5分.
=
=
…………6分.
當x=4時，原式=
…………7分
提示：本題屬開放題，答案不唯一。在選取x值時，注意必須符合x>3這一條件。
16．解：設原計劃參加植樹的學生有
人，則實際參加植樹的學生有1.5，依題意得：
………2分
…………5分
解得
，
經檢驗x=30是原方程的根，∴
…………6分
答：實際參加這次植樹的學生有45人． …………7分
17．解：作AD⊥BC交BC延長線于D， …………2分
設AD=，在Rt△ACD中，∠CAD=30°
∴CD=
。 …………4分
在Rt△ABD中，∠ABD=30°
∴BD=
∵BC=8
x=4
≈6.928 ∵6.928海里<7海里 …………6分
∴有觸礁危險。
答：有觸礁危險。 …………7分
18．根據具體情況給分。
四、解答題
19．解：(1)設紅球的個數為，………………………………1分
由題意得，
……………………………4分
解得， 
.
答：口袋中紅球的個數是1. ……………………………5分
(2)小明的認為不對. ……………………………………6分
樹狀圖如下：
…………8分
∴ 
，
，
.
∴ 小明的認為不對. …………9分
20．解：可組成方程組：
………………2分
(1)＋(2)得：
………………4分
∴
………………6分
把代入(2)得：
………………8分
∴原方程組的解為
………………9分
答案不唯一，其它按此參考給分
21．猜想：BE∥DF BE=DF ………………4分.
證明：在平行四邊形ABCD中，AB=CD、AB∥CD
∴∠BAC=∠DCA
又∵ AF=CE
∴AE=CF
∴△ABE≌△CDF ………………7分.
∴BE=DF ∠AEB=∠CFD
∴∠BEF=∠DFE
∴BE∥DF ………………9分.
五、解答題
22.．解：(1)
，
°，
°． ……………2分
又
平分
，
°．……………4分
，
°．
°， ………………6分
是圓的直徑，
． ………………7分
四邊形
的周長為
cm，
cm，
cm．
此圓的半徑為
cm． ………………8分
(2)設
的中點為
，由(1)可知即為圓心．
連接
，過作
于
．……………9分
在
中，
，
cm．
(cm2)． ………………10分
≈0.3(cm2)……12分
23. 解：(1) 如圖：
，
；…………………………4分
(2) (b，a) ； …………………………6分
(3) 由(2)得，D(1,-3) 關于直線 l 的對稱點
的坐標為(－3,1)，連接E交
直線 l 于點Q，此時點Q到D、E兩點的距離之和最小 ……………8分
設過(-3,1) 、E(-1,-4)的直線的解析式為
，則
，∴
，
∴
．
…………………………10分
由
得
∴所求Q點的坐標為(
，) …………12分
24．解：(1)依據題意
∵AP=AD=4，AE=2
∴EP=
∴P點坐標為(2
，2) ……………………4分
設DM=x，則MP=x，過M作MN⊥EF，垂足為N，則MN=2，
PN=2－x
在Rt△MNP中，22＋(2－x)2=x2
解之得：x=
∴M點坐標為(，4) ………8分
(2)設折痕AM所在直線的解析式為y=kx(k≠0)，則4=
k
k=
∴折痕AM所在直線的解析式為y=x ………10分
(3)H1(－2，－2)，H2(
，2)，H3(2，2)，H4(2，6) ………12分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com