
題目列表(包括答案和解析)
已知 ,
,
求  和
和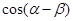 的值.
的值.
【解析】利用三角恒等變換得到函數值,
由于
得

解析: 由

得

已知在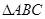 中,
中,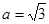 ,
,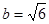 ,
,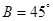 ,解這個三角形;
,解這個三角形;
【解析】本試題主要考查了正弦定理的運用。由正弦定理得到: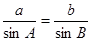
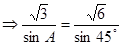 ,然后又
,然后又 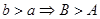
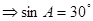
又 再又
再又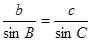 得到c。
得到c。
解:由正弦定理得到: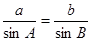
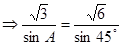
又 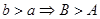
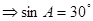 ……4分
……4分
又 ……8分
……8分
又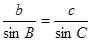
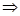
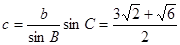
求由拋物線 與直線
與直線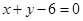 及
及 所圍成圖形的面積.
所圍成圖形的面積.
【解析】首先利用已知函數和拋物線作圖,然后確定交點坐標,然后利用定積分表示出面積為 ,所以得到
,所以得到 ,由此得到結論為
,由此得到結論為
解:設所求圖形面積為 ,則
,則

 =
= .即所求圖形面積為
.即所求圖形面積為 .
.

已知指數函數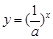 ,當
,當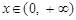 時,有
時,有 ,解關于x的不等式
,解關于x的不等式
【解析】本試題主要考查了指數函數,對數函數性質的運用。首先利用指數函數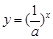 ,當
,當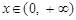 時,有
時,有 ,,得到
,,得到 ,從而
,從而
 等價于
等價于 ,聯立不等式組可以解得
,聯立不等式組可以解得
解:∵ 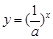 在
在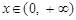 時,有
時,有 ,
∴
,
∴  。
。
于是由 ,得
,得 ,
,
解得 ,
∴ 不等式的解集為
,
∴ 不等式的解集為 。
。
已知 ,(其中
,(其中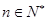 )
)
⑴求 及
及 ;
;
⑵試比較 與
與 的大小,并說明理由.
的大小,并說明理由.
【解析】第一問中取 ,則
,則 ;
…………1分
;
…………1分
對等式兩邊求導,得
取 ,則
,則 得到結論
得到結論
第二問中,要比較 與
與 的大小,即比較:
的大小,即比較: 與
與 的大小,歸納猜想可得結論當
的大小,歸納猜想可得結論當 時,
時, ;
;
當 時,
時, ;
;
當 時,
時, ;
;
猜想:當 時,
時, 運用數學歸納法證明即可。
運用數學歸納法證明即可。
解:⑴取 ,則
,則 ;
…………1分
;
…………1分
對等式兩邊求導,得 ,
,
取 ,則
,則 。 …………4分
。 …………4分
⑵要比較 與
與 的大小,即比較:
的大小,即比較: 與
與 的大小,
的大小,
當 時,
時, ;
;
當 時,
時, ;
;
當 時,
時, ;
…………6分
;
…………6分
猜想:當 時,
時, ,下面用數學歸納法證明:
,下面用數學歸納法證明:
由上述過程可知, 時結論成立,
時結論成立,
假設當 時結論成立,即
時結論成立,即 ,
,
當 時,
時,
而
∴
即 時結論也成立,
時結論也成立,
∴當 時,
時, 成立。
…………11分
成立。
…………11分
綜上得,當 時,
時, ;
;
當 時,
時, ;
;
當 時,
時,
1. 構造向量 ,
, ,所以
,所以 ,
, .由數量積的性質
.由數量積的性質 ,得
,得 ,即
,即 的最大值為2.
的最大值為2.
2. ∵ ,令
,令 得
得 ,所以
,所以 ,當
,當 時,
時, ,當
,當 時,
時, ,所以當
,所以當 時,
時, .
.
3.∵ ,∴
,∴ ,
, ,又
,又 ,∴
,∴ ,則
,則 ,所以周期
,所以周期 .作出
.作出 在
在 上的圖象知:若
上的圖象知:若 ,滿足條件的
,滿足條件的 (
( )存在,且
)存在,且 ,
, 關于直線
關于直線 對稱,
對稱, ,
, 關于直線
關于直線 對稱,∴
對稱,∴ ;若
;若 ,滿足條件的
,滿足條件的 (
( )存在,且
)存在,且 ,
, 關于直線
關于直線 對稱,
對稱, ,
, 關于直線
關于直線 對稱,
對稱,
 ∴
∴ .
.
4. 不等式 (
( )表示的區域是如圖所示的菱形的內部,
)表示的區域是如圖所示的菱形的內部,
∵
 ,
,
當 ,點
,點 到點
到點 的距離最大,此時
的距離最大,此時 的最大值為
的最大值為 ;
;
當 ,點
,點 到點
到點 的距離最大,此時
的距離最大,此時 的最大值為3.
的最大值為3.
5. 由于已有兩人分別抽到5和14兩張卡片,則另外兩人只需從剩下的18張卡片中抽取,共有 種情況.抽到5 和14的兩人在同一組,有兩種情況:
種情況.抽到5 和14的兩人在同一組,有兩種情況:
(1) 5 和14 為較小兩數,則另兩人需從15~20這6張中各抽1張,有 種情況;
種情況;
(2) 5 和14 為較大兩數,則另兩人需從1~4這4張中各抽1張,有 種情況.
種情況.
于是,抽到5 和14 兩張卡片的兩人在同一組的概率為 .
.
 6. ∵
6. ∵ ,∴
,∴ ,
,
設 ,
, ,則
,則 .
.
作出該不等式組表示的平面區域(圖中的陰影部分 ).
).
令 ,則
,則 ,它表示斜率為
,它表示斜率為 的一組平行直線,易知,當它經過點
的一組平行直線,易知,當它經過點 時,
時, 取得最小值.
取得最小值.
解方程組 ,得
,得 ,∴
,∴
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com