
題目列表(包括答案和解析)
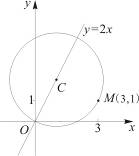
已知拋物線C: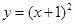 與圓
與圓 有一個公共點A,且在A處兩曲線的切線與同一直線l
有一個公共點A,且在A處兩曲線的切線與同一直線l
(I) 求r;
(II) 設(shè)m、n是異于l且與C及M都相切的兩條直線,m、n的交點為D,求D到l的距離。
【解析】本試題考查了拋物線與圓的方程,以及兩個曲線的公共點處的切線的運用,并在此基礎(chǔ)上求解點到直線的距離。
【點評】該試題出題的角度不同于平常,因為涉及的是兩個二次曲線的交點問題,并且要研究兩曲線在公共點出的切線,把解析幾何和導(dǎo)數(shù)的工具性結(jié)合起來,是該試題的創(chuàng)新處。另外對于在第二問中更是難度加大了,出現(xiàn)了另外的兩條公共的切線,這樣的問題對于我們以后的學(xué)習(xí)也是一個需要練習(xí)的方向。

△ABC中,內(nèi)角A、B、C成等差數(shù)列,其對邊a、b、c滿足 ,求A。
,求A。
【解析】本試題主要考查了解三角形的運用,
因為

【點評】該試題從整體來看保持了往年的解題風(fēng)格,依然是通過邊角的轉(zhuǎn)換,結(jié)合了三角形的內(nèi)角和定理的知識,以及正弦定理和余弦定理,求解三角形中的角的問題。試題整體上比較穩(wěn)定,思路也比較容易想,先將利用等差數(shù)列得到角B,然后利用余弦定理求解運算得到A。
若 則給出的數(shù)列{
則給出的數(shù)列{ 第34項為( )
第34項為( )
A. 1/103 B.1/100 C.103 D.100
求圓心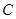 在直線
在直線 上,且經(jīng)過原點及點
上,且經(jīng)過原點及點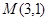 的圓
的圓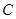 的標(biāo)準(zhǔn)方程.
的標(biāo)準(zhǔn)方程.
【解析】本試題主要考查的圓的方程的求解,利用圓心和半徑表示圓,首先設(shè)圓心C的坐標(biāo)為( ),然后利用
),然后利用 ,得到
,得到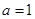 ,從而圓心
,從而圓心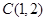 ,半徑
,半徑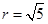 .可得原點 標(biāo)準(zhǔn)方程。
.可得原點 標(biāo)準(zhǔn)方程。
解:設(shè)圓心C的坐標(biāo)為( ),...........2分
),...........2分
則 ,即
,即
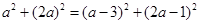 ,解得
,解得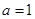 ........4分
........4分
所以圓心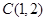 ,半徑
,半徑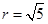 ...........8分
...........8分
故圓C的標(biāo)準(zhǔn)方程為: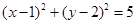 .......10分
.......10分
已知函數(shù)
(I) 討論f(x)的單調(diào)性;
(II) 設(shè)f(x)有兩個極值點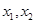 若過兩點
若過兩點 的直線I與x軸的交點在曲線
的直線I與x軸的交點在曲線 上,求α的值。
上,求α的值。
【解析】本試題考查了導(dǎo)數(shù)在研究函數(shù)中的運用。第一就是三次函數(shù),通過求解導(dǎo)數(shù),求解單調(diào)區(qū)間。另外就是運用極值的概念,求解參數(shù)值的運用。
【點評】試題分為兩問,題面比較簡單,給出的函數(shù)比較常規(guī),,這一點對于同學(xué)們來說沒有難度但是解決的關(guān)鍵還是要看導(dǎo)數(shù)的符號的實質(zhì)不變,求解單調(diào)區(qū)間。第二問中,運用極值的問題,和直線方程的知識求解交點,得到參數(shù)的值。
(1)

1. 構(gòu)造向量學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image369.gif) ,
,學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image371.gif) ,所以
,所以學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image373.gif) ,
,學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image375.gif) .由數(shù)量積的性質(zhì)
.由數(shù)量積的性質(zhì)學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image377.gif) ,得
,得學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image379.gif) ,即
,即學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image329.gif) 的最大值為2.
的最大值為2.
2. ∵學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image381.gif) ,令
,令學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image383.gif) 得
得學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image385.gif) ,所以
,所以學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image387.gif) ,當(dāng)
,當(dāng)學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image389.gif) 時,
時,學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image391.gif) ,當(dāng)
,當(dāng)學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image393.gif) 時,
時,學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image395.gif) ,所以當(dāng)
,所以當(dāng)學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image387.gif) 時,
時,學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image397.gif) .
.
3.∵學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image399.gif) ,∴
,∴學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image401.gif) ,
,學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image403.gif) ,又
,又學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image337.gif) ,∴
,∴學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image405.gif) ,則
,則學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image407.gif) ,所以周期
,所以周期學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image409.gif) .作出
.作出學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image411.gif) 在
在學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image413.gif) 上的圖象知:若
上的圖象知:若學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image415.gif) ,滿足條件的
,滿足條件的學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image341.gif) (
(學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image347.gif) )存在,且
)存在,且學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image417.gif) ,
,學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image419.gif) 關(guān)于直線
關(guān)于直線學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image421.gif) 對稱,
對稱,學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image423.gif) ,
,學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image425.gif) 關(guān)于直線
關(guān)于直線學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image427.gif) 對稱,∴
對稱,∴學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image429.gif) ;若
;若學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image431.gif) ,滿足條件的
,滿足條件的學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image341.gif) (
(學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image347.gif) )存在,且
)存在,且學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image417.gif) ,
,學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image419.gif) 關(guān)于直線
關(guān)于直線學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image433.gif) 對稱,
對稱,學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image423.gif) ,
,學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image425.gif) 關(guān)于直線
關(guān)于直線學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image435.gif) 對稱,
對稱,
學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image437.jpg) ∴
∴學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image439.gif) .
.
4. 不等式學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image354.gif) (
(學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image356.gif) )表示的區(qū)域是如圖所示的菱形的內(nèi)部,
)表示的區(qū)域是如圖所示的菱形的內(nèi)部,
∵學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image358.gif)
學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image441.gif) ,
,
當(dāng)學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image443.gif) ,點
,點學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image445.gif) 到點
到點學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image447.gif) 的距離最大,此時
的距離最大,此時學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image358.gif) 的最大值為
的最大值為學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image449.gif) ;
;
當(dāng)學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image451.gif) ,點
,點學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image453.gif) 到點
到點學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image447.gif) 的距離最大,此時
的距離最大,此時學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image358.gif) 的最大值為3.
的最大值為3.
5. 由于已有兩人分別抽到5和14兩張卡片,則另外兩人只需從剩下的18張卡片中抽取,共有學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image455.gif) 種情況.抽到5 和14的兩人在同一組,有兩種情況:
種情況.抽到5 和14的兩人在同一組,有兩種情況:
(1) 5 和14 為較小兩數(shù),則另兩人需從15~20這6張中各抽1張,有學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image457.gif) 種情況;
種情況;
(2) 5 和14 為較大兩數(shù),則另兩人需從1~4這4張中各抽1張,有學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image459.gif) 種情況.
種情況.
于是,抽到5 和14 兩張卡片的兩人在同一組的概率為學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image461.gif) .
.
學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image463.gif) 6. ∵
6. ∵學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image365.gif) ,∴
,∴學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image465.gif) ,
,
設(shè)學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image467.gif) ,
,學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image469.gif) ,則
,則學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image471.gif) .
.
作出該不等式組表示的平面區(qū)域(圖中的陰影部分學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image473.gif) ).
).
令學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image475.gif) ,則
,則學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image477.gif) ,它表示斜率為
,它表示斜率為學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image193.gif) 的一組平行直線,易知,當(dāng)它經(jīng)過點
的一組平行直線,易知,當(dāng)它經(jīng)過點學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image016.gif) 時,
時,學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image316.gif) 取得最小值.
取得最小值.
解方程組學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image482.gif) ,得
,得學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image484.gif) ,∴
,∴學(xué)高考解題技巧---數(shù)學(xué)題型專題--填空題的解法.files/image486.gif)
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com