
題目列表(包括答案和解析)
若函數(shù)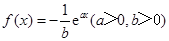 的圖象在
的圖象在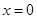 處的切線與圓
處的切線與圓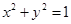 相切,則
相切,則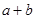 的最大值是( )
的最大值是( )
(A)4 (B)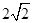 (C)2
(D)
(C)2
(D)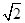
若函數(shù) 的圖象在
的圖象在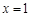 處的切線
處的切線 過點
過點 ,且
,且 與圓
與圓 相交,則點
相交,則點 與圓
與圓 的位置關(guān)系是
的位置關(guān)系是
A.點在圓內(nèi) B.點在圓外
C.點在圓上 D.不能確定
若函數(shù)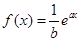 的圖象在
的圖象在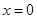 處的切線
處的切線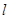 與圓
與圓 相離,則
相離,則 與圓C的位置關(guān)系是
與圓C的位置關(guān)系是
A. 在圓內(nèi) B. 在圓上
C. 在圓外 D.不確定,與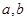 的取值有關(guān)
的取值有關(guān)
若函數(shù) 的圖象在
的圖象在 處的切線
處的切線 與圓
與圓 相離,則點
相離,則點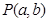 與圓C的位置關(guān)系是 ( )
與圓C的位置關(guān)系是 ( )
A.點在圓外 B.點在圓內(nèi) C.點在圓上 D.不能確定
(本小題滿分15分)
已知函數(shù)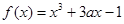 ,
,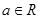 .
.
(Ⅰ)若函數(shù)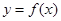 的圖象在
的圖象在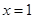 處的切線與直線
處的切線與直線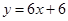 平行,求實數(shù)
平行,求實數(shù)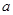 的值;
的值;
(Ⅱ)設(shè)函數(shù)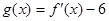 ,對任意的
,對任意的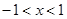 ,都有
,都有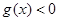 成立,求實數(shù)
成立,求實數(shù)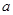 的取值范圍;
的取值范圍;
(Ⅲ)當(dāng)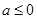 時,請問:是否存在整數(shù)
時,請問:是否存在整數(shù)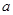 的值,使方程
的值,使方程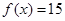 有且只有一個實根?若存在,求出整數(shù)
有且只有一個實根?若存在,求出整數(shù)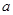 的值;否則,請說明理由.
的值;否則,請說明理由.
2008年7月
【課前預(yù)習(xí)】
答案: 1、 ; 2、B.【試題分析】令
; 2、B.【試題分析】令 ,可求得:
,可求得:
 。易知函數(shù)
。易知函數(shù) 的零點所在區(qū)間為
的零點所在區(qū)間為 。
。
3、 ; 4、-4。
; 4、-4。
四.典例解析
題型1:方程的根與函數(shù)零點
例1. 分析:利用函數(shù)零點的存在性定理或圖像進行判斷。
解析:(1)方法一:

 ∴
∴
故 。
。
方法二:
令 解得
解得 ,
,
所以函數(shù) 。
。
(2)∵ ,
,
∴ 。
。
(3)∵ ,
,
 ,
,
∴ ,故
,故 在
在 存在零點。
存在零點。
評析:函數(shù)的零點存在性問題常用的辦法有三種:一是定理;二是用方程;三是用圖像
例2. 解析:(1)方法一令
 則根據(jù)選擇支可以求得
則根據(jù)選擇支可以求得
 <0;
<0; <0;
<0; >0.因為
>0.因為 <0可得零點在(2,3)內(nèi)選C
<0可得零點在(2,3)內(nèi)選C
 方法二:在同一平面直角坐標(biāo)系中,畫出函數(shù)y=lgx與y=-x+3的圖象(如圖)。它們的交點橫坐標(biāo)
方法二:在同一平面直角坐標(biāo)系中,畫出函數(shù)y=lgx與y=-x+3的圖象(如圖)。它們的交點橫坐標(biāo) ,顯然在區(qū)間(1,3)內(nèi),由此可排除A,D
,顯然在區(qū)間(1,3)內(nèi),由此可排除A,D 至于選B還是選C,由于畫圖精確性的限制,單憑直觀就比較困難了。實際上這是要比較
至于選B還是選C,由于畫圖精確性的限制,單憑直觀就比較困難了。實際上這是要比較 與2的大小。當(dāng)x=2時,lgx=lg2,3-x=1。由于lg2<1,因此
與2的大小。當(dāng)x=2時,lgx=lg2,3-x=1。由于lg2<1,因此 >2,從而判定
>2,從而判定 ∈(2,3),故本題應(yīng)選C
∈(2,3),故本題應(yīng)選C
 (2)原方程等價于
(2)原方程等價于
即
構(gòu)造函數(shù) 和
和 ,作出它們的圖像,易知平行于x軸的直線與拋物線的交點情況可得:
,作出它們的圖像,易知平行于x軸的直線與拋物線的交點情況可得:
①當(dāng) 或
或 時,原方程有一解;
時,原方程有一解;
②當(dāng) 時,原方程有兩解;
時,原方程有兩解;
③當(dāng) 或
或 時,原方程無解。
時,原方程無解。
點評:圖象法求函數(shù)零點,考查學(xué)生的數(shù)形結(jié)合思想。本題是通過構(gòu)造函數(shù)用數(shù)形結(jié)合法求方程lgx+x=3解所在的區(qū)間。數(shù)形結(jié)合,要在結(jié)合方面下功夫。不僅要通過圖象直觀估計,而且還要計算 的鄰近兩個函數(shù)值,通過比較其大小進行判斷
的鄰近兩個函數(shù)值,通過比較其大小進行判斷
題型2:零點存在性定理
例3.解析:(1)函數(shù)f(x)=x-ln(x+m),x∈(-m,+∞)連續(xù),且

當(dāng)x∈(-m,1-m)時,f ’(x)<0,f(x)為減函數(shù),f(x)>f(1-m)
當(dāng)x∈(1-m, +∞)時,f ’(x)>0,f(x)為增函數(shù),f(x)>f(1-m)
根據(jù)函數(shù)極值判別方法,f(1-m)=1-m為極小值,而且
對x∈(-m, +∞)都有f(x)≥f(1-m)=1-m
故當(dāng)整數(shù)m≤1時,f(x) ≥1-m≥0
(2)證明:由(I)知,當(dāng)整數(shù)m>1時,f(1-m)=1-m<0,
函數(shù)f(x)=x-ln(x+m),在 上為連續(xù)減函數(shù).
上為連續(xù)減函數(shù).

由所給定理知,存在唯一的
而當(dāng)整數(shù)m>1時,

類似地,當(dāng)整數(shù)m>1時,函數(shù)f(x)=x-ln(x+m),在 上為連續(xù)增函數(shù)且 f(1-m)與
上為連續(xù)增函數(shù)且 f(1-m)與 異號,由所給定理知,存在唯一的
異號,由所給定理知,存在唯一的
故當(dāng)m>1時,方程f(x)=0在 內(nèi)有兩個實根。
內(nèi)有兩個實根。
點評:本題以信息給予的形式考察零點的存在性定理。解決該題的解題技巧主要在區(qū)間的放縮和不等式的應(yīng)用上。
例4. 解析:由零點存在性定理可知選項D不正確;對于選項B,可通過反例“ 在區(qū)間
在區(qū)間 上滿足
上滿足 ,但其存在三個解
,但其存在三個解 ”推翻;同時選項A可通過反例“
”推翻;同時選項A可通過反例“ 在區(qū)間
在區(qū)間 上滿足
上滿足 ,但其存在兩個解
,但其存在兩個解 ”;選項D正確,見實例“
”;選項D正確,見實例“ 在區(qū)間
在區(qū)間 上滿足
上滿足 ,但其不存在實數(shù)解”。
,但其不存在實數(shù)解”。
點評:該問題詳細(xì)介紹了零點存在性定理的理論基礎(chǔ)。
題型3:二分法的概念
例5. 解析:如果函數(shù)在某區(qū)間滿足二分法題設(shè),且在區(qū)間內(nèi)存在兩個及以上的實根,二分法只可能求出其中的一個,只要限定了近似解的范圍就可以得到函數(shù)的近似解,二分法的實施滿足零點存在性定理,在區(qū)間內(nèi)一定存在零點,甚至有可能得到函數(shù)的精確零點。
點評:該題深入解析了二分法的思想方法。
例6.解析:由四舍五入的原則知道,當(dāng) 時,精度達到
時,精度達到 。此時差限
。此時差限 是0.0005,選項為C。
是0.0005,選項為C。
點評:該題考察了差限的定義,以及它對精度的影響。
題型4:應(yīng)用“二分法”求函數(shù)的零點和方程的近似解
例7. 解析:原方程即 。令
。令 ,
,
用計算器做出如下對應(yīng)值表
x
-2
-1
0
1
2
f(x)
2.5820
3.0530
27918
1.0794
-4.6974
觀察上表,可知零點在(1,2)內(nèi)
取區(qū)間中點 =1.5,且
=1.5,且 ,從而,可知零點在(1,1.5)內(nèi);
,從而,可知零點在(1,1.5)內(nèi);
再取區(qū)間中點 =1.25,且
=1.25,且 ,從而,可知零點在(1.25,1.5)內(nèi);
,從而,可知零點在(1.25,1.5)內(nèi);
同理取區(qū)間中點 =1.375,且
=1.375,且 ,從而,可知零點在(1.25,1.375)內(nèi);
,從而,可知零點在(1.25,1.375)內(nèi);
由于區(qū)間(1.25,1.375)內(nèi)任一值精確到0.1后都是1.3。故結(jié)果是1.3。
點評:該題系統(tǒng)的講解了二分法求方程近似解的過程,通過本題學(xué)會借助精度終止二分法的過程。
例8. 分析:本例除借助計算器或計算機確定方程解所在的大致區(qū)間和解的個數(shù)外,你是否還可以想到有什么方法確定方程的根的個數(shù)?
略解:圖象在閉區(qū)間 ,
, 上連續(xù)的單調(diào)函數(shù)
上連續(xù)的單調(diào)函數(shù) ,在
,在 ,
, 上至多有一個零點。
上至多有一個零點。
點評:①第一步確定零點所在的大致區(qū)間 ,
, ,可利用函數(shù)性質(zhì),也可借助計算機或計算器,但盡量取端點為整數(shù)的區(qū)間,盡量縮短區(qū)間長度,通常可確定一個長度為1的區(qū)間;
,可利用函數(shù)性質(zhì),也可借助計算機或計算器,但盡量取端點為整數(shù)的區(qū)間,盡量縮短區(qū)間長度,通常可確定一個長度為1的區(qū)間;
②建議列表樣式如下:
零點所在區(qū)間
中點函數(shù)值
區(qū)間長度
[1,2]
 >0
>0
1
[1,1.5]
 <0
<0
0.5
[1.25,1.5]
 <0
<0
0.25
如此列表的優(yōu)勢:計算步數(shù)明確,區(qū)間長度小于精度時,即為計算的最后一步。
題型5:一元二次方程的根與一元二次函數(shù)的零點
例9. 分析:從二次方程的根分布看二次函數(shù)圖像特征,再根據(jù)圖像特征列出對應(yīng)的不等式(組)。
解析:(1)設(shè) ,
,
由 ,知
,知 ∴
∴ ,
,
∴
(2)令
 ∴
∴ ,
,
且 ,∴
,∴ ,∴
,∴ ,
,
綜上, 。
。
評析:二次方程、二次函數(shù)、二次不等式三者密不可分。
例10.解析:設(shè) ,則
,則 的二根為
的二根為 和
和 。
。
(1)由 及
及 ,可得
,可得  ,即
,即 ,
,
即 兩式相加得
兩式相加得 ,所以,
,所以, ;
;
(2)由 , 可得
, 可得  。
。
又 ,所以
,所以 同號。
同號。
∴  ,
, 等價于
等價于
或 ,
,
即  或
或
解之得  或
或 。
。
點評:條件 實際上給出了
實際上給出了 的兩個實數(shù)根所在的區(qū)間,因此可以考慮利用上述圖像特征去等價轉(zhuǎn)化。
的兩個實數(shù)根所在的區(qū)間,因此可以考慮利用上述圖像特征去等價轉(zhuǎn)化。
【課外作業(yè)】
1. 答案:A,令 即可;
即可;
2. 答案:B;
3.答案:C,由 可得
可得 關(guān)于
關(guān)于 對稱,∴
對稱,∴ ,∴
,∴ ∴
∴ ,∴
,∴ ,∵
,∵ ,∴
,∴ 。
。
4、 答案:D, ∵ ,∴
,∴ ∴
∴
 , ∴
, ∴
5. 答案:C,先求出 ,根據(jù)單調(diào)性求解;
,根據(jù)單調(diào)性求解;
五.思維總結(jié)
1.函數(shù)零點的求法:
①(代數(shù)法)求方程 的實數(shù)根;
的實數(shù)根;
②(幾何法)對于不能用求根公式的方程,可以將它與函數(shù) 的圖象聯(lián)系起來,并利用函數(shù)的性質(zhì)找出零點。
的圖象聯(lián)系起來,并利用函數(shù)的性質(zhì)找出零點。
2.解決二次函數(shù)的零點分布問題要善于結(jié)合圖像,從判別式、韋達定理、對稱軸、區(qū)間端點函數(shù)值的正負(fù)、二次函數(shù)圖像的開口方向等方面去考慮使結(jié)論成立的所有條件。函數(shù)與方程、不等式聯(lián)系密切,聯(lián)系的方法就是數(shù)形結(jié)合。
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com