
題目列表(包括答案和解析)
(本題滿分16分,其中第(1)小題4分,第(2)小題8分,第(3)小題4分)
設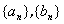 是兩個數列,
是兩個數列, 為直角坐標平面上的點.對
為直角坐標平面上的點.對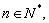 若三點
若三點 共線,
共線,
(1)求數列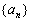 的通項公式;
的通項公式;
(2)若數列{ }滿足:
}滿足: ,其中
,其中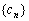 是第三項為8,公比為4的等比數列.求證:點列
是第三項為8,公比為4的等比數列.求證:點列 (1,
(1,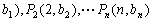 在同一條直線上;
在同一條直線上;
(3)記數列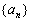 、{
、{ }的前
}的前 項和分別為
項和分別為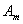 和
和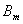 ,對任意自然數
,對任意自然數 ,是否總存在與
,是否總存在與 相關的自然數
相關的自然數 ,使得
,使得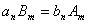 ?若存在,求出
?若存在,求出 與
與 的關系,若不存在,請說明理由.
的關系,若不存在,請說明理由.
給出下列四個函數:①f(x)=lnx;②f(x)=x2+1;③f(x)=e-x;④f(x)=sinx,其中滿足:“對任意x1、x2∈(1,2),x1≠x2,不等式|f(x1)-f(x2)|<|x1-x2|總成立”的是________.(將正確的序中與填在橫線上)
我們知道,如果定義在某區間上的函數![]() 滿足對該區間上的任意兩個數
滿足對該區間上的任意兩個數![]() 、
、![]() ,
,
總有不等式![]() 成立,則稱函數
成立,則稱函數![]() 為該區間上的向上凸函數(簡稱上凸).
為該區間上的向上凸函數(簡稱上凸).
類比上述定義,對于數列![]() ,如果對任意正整數
,如果對任意正整數![]() ,總有不等式:
,總有不等式:![]() 成立,
成立,
則稱數列![]() 為向上凸數列(簡稱上凸數列). 現有數列
為向上凸數列(簡稱上凸數列). 現有數列![]() 滿足如下兩個條件:
滿足如下兩個條件:
(1)數列![]() 為上凸數列,且
為上凸數列,且![]() ;
;
(2)對正整數![]() (
(![]() ),都有
),都有![]() ,其中
,其中![]() .
.
則數列![]() 中的第五項
中的第五項![]() 的取值范圍為 ★ .
的取值范圍為 ★ .
我們知道,如果定義在某區間上的函數![]() 滿足對該區間上的任意兩個數
滿足對該區間上的任意兩個數![]() 、
、![]() ,總有不等式
,總有不等式![]() 成立,則稱函數
成立,則稱函數![]() 為該區間上的向上凸函數(簡稱上凸). 類比上述定義,對于數列
為該區間上的向上凸函數(簡稱上凸). 類比上述定義,對于數列![]() ,如果對任意正整數
,如果對任意正整數![]() ,總有不等式:
,總有不等式:![]() 成立,則稱數列
成立,則稱數列![]() 為向上凸數列(簡稱上凸數列). 現有數列
為向上凸數列(簡稱上凸數列). 現有數列![]() 滿足如下兩個條件:
滿足如下兩個條件:
(1)數列![]() 為上凸數列,且
為上凸數列,且![]() ;
;
(2)對正整數![]() (
(![]() ),都有
),都有![]() ,其中
,其中![]() .
.
則數列![]() 中的第五項
中的第五項![]() 的取值范圍為 ▲ .
的取值范圍為 ▲ .
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| an+an+2 |
| 2 |
一、選擇題 ABCBD DBCDC CC
二、填空題
13.6; ;14.
;14. ;15.
;15. ,1)∪(1,+∞);16。①③④
,1)∪(1,+∞);16。①③④
三、解答題
17. 解:(1)∵  , 且與向量
, 且與向量 所成角為
所成角為
∴  ,
∴
,
∴  ,
,
又 ,∴
,∴
 ,即
,即 。
。
(2)由(1)可得:
∴ 



∵  ,∴
,∴
 ,
,
∴  ,∴
當
,∴
當 =1時,A=
=1時,A=
∴AB=2, 則
18.解:(1)P=
(2)隨機變量 的取值為0, 1, 2, 3.
的取值為0, 1, 2, 3.
由n次獨立重復試驗概率公式 得
得




隨機變量 的分布列是
的分布列是

0
1
2
3





 的數學期望是
的數學期望是 
19.(I)解:取CE中點P,連結FP、BP,
∵F為CD的中點,∴FP//DE,且FP=
又AB//DE,且AB= ,∴AB//FP,且AB=FP,
,∴AB//FP,且AB=FP,
∴ABPF為平行四邊形,∴AF//BP。…………2分
又∵AF 平面BCE,BP
平面BCE,BP 平面BCE,∴AF//平面BCE。
…………4分
平面BCE,∴AF//平面BCE。
…………4分
(II)∵△ACD為正三角形,∴AF⊥CD。
∵AB⊥平面ACD,DE//AB,∴DE⊥平面ACD,又AF 平面ACD,
平面ACD,
∴DE⊥AF。又AF⊥CD,CD∩DE=D,∴AF⊥平面CDE。 …………6分
又BP//AF,∴BP⊥平面CDE。又∵BP 平面BCE,
平面BCE,
∴平面BCE⊥平面CDE。 …………8分
(III)由(II),以F為坐標原點,FA,FD,FP所在的直線分別為x,y,z軸(如圖),建立空間直角坐標系F―xyz.設AC=2,
則C(0,―1,0), ………………9分
………………9分
 ……10分
……10分
顯然, 為平面ACD的法向量。
為平面ACD的法向量。
設平面BCE與平面ACD所成銳二面角為
 ,即平面BCE與平面ACD所成銳二面角為45°。…………12分
,即平面BCE與平面ACD所成銳二面角為45°。…………12分
20.(1)

 時,
時, ,即
,即
當 時,
時,
即
 在
在 上是減函數的充要條件為
上是減函數的充要條件為 ………(4分)
………(4分)
(2)由(1)知,當 時
時 為減函數,
為減函數, 的最大值為
的最大值為 ;
;
當 時,
時,
 當
當 時
時 ,當
,當 時
時
即在 上
上 是增函數,在
是增函數,在 上
上 是減函數,
是減函數, 時
時 取最大值,最大值為
取最大值,最大值為 即
即 …(8分)
…(8分)
(3)在(1)中取 ,即
,即
由(1)知 在
在 上是減函數
上是減函數
 ,即
,即
 ,解得:
,解得: 或
或
故所求不等式的解集為[ ……………(12分)
……………(12分)
21. 解:(1) ,
, ,
,
又 ,∴數列
,∴數列 是首項為
是首項為 ,公比為
,公比為 的等比數列.
的等比數列.
(2)依(Ⅰ)的結論有 ,即
,即 .
.
 .
.
 .
.
(3) ,又由(Ⅱ)有
,又由(Ⅱ)有
 .
.
則
 (
(  ) =
) = 
=( 1- )<∴ 對任意的
)<∴ 對任意的 ,
, .
.
22.解:(I)由條件知: ………2分
………2分
得 ………4分
………4分
(II)依條件有: ………5分, 由
………5分, 由

 8分
8分

由 ,
, ………10分
………10分
由弦長公式得
由

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com