
題目列表(包括答案和解析)
在平面直角坐標系xOy中,以O為極點,X軸的正半軸為極軸,取與直角坐標系相同的長度單位建立極坐標系.曲線C1的參數方程為: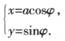 (
(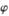 為參數);射線C2的極坐標方程為:
為參數);射線C2的極坐標方程為: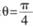 ,且射線C2與曲線C1的交點的橫坐標為
,且射線C2與曲線C1的交點的橫坐標為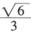
(I )求曲線C1的普通方程;
(II)設A、B為曲線C1與y軸的兩個交點,M為曲線C1上不同于A、B的任意一點,若直線AM與MB分別與x軸交于P,Q兩點,求證|OP|.|OQ|為定值.
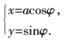 (
(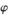 為參數);射線C2的極坐標方程為:
為參數);射線C2的極坐標方程為: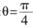 ,且射線C2與曲線C1的交點的橫坐標為
,且射線C2與曲線C1的交點的橫坐標為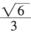
在復平面內,  是原點,向量
是原點,向量 對應的復數是
對應的復數是 ,
, =2+i。
=2+i。
(Ⅰ)如果點A關于實軸的對稱點為點B,求向量 對應的復數
對應的復數 和
和 ;
;
(Ⅱ)復數 ,
, 對應的點C,D。試判斷A、B、C、D四點是否在同一個圓上?并證明你的結論。
對應的點C,D。試判斷A、B、C、D四點是否在同一個圓上?并證明你的結論。
【解析】第一問中利用復數的概念可知得到由題意得,A(2,1) ∴B(2,-1)
∴  =(0,-2)
∴
=(0,-2)
∴ =-2i ∵
=-2i ∵  (2+i)(-2i)=2-4i,
∴
(2+i)(-2i)=2-4i,
∴  =
=
第二問中,由題意得, =(2,1)
∴
=(2,1)
∴
同理 ,所以A、B、C、D四點到原點O的距離相等,
,所以A、B、C、D四點到原點O的距離相等,
∴A、B、C、D四點在以O為圓心, 為半徑的圓上
為半徑的圓上
(Ⅰ)由題意得,A(2,1) ∴B(2,-1)
∴  =(0,-2)
∴
=(0,-2)
∴ =-2i 3分
=-2i 3分
∵  (2+i)(-2i)=2-4i,
∴
(2+i)(-2i)=2-4i,
∴  =
= 2分
2分
(Ⅱ)A、B、C、D四點在同一個圓上。 2分
證明:由題意得, =(2,1)
∴
=(2,1)
∴
同理 ,所以A、B、C、D四點到原點O的距離相等,
,所以A、B、C、D四點到原點O的距離相等,
∴A、B、C、D四點在以O為圓心, 為半徑的圓上
為半徑的圓上
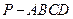
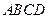
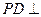
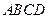
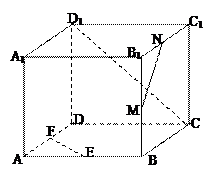
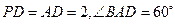 ,
, 、
、 分別為
分別為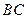 、
、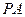 的中點。
的中點。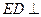 平面
平面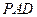 ;
;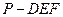 的體積;
的體積;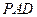 與平面
與平面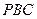 所成的銳二面角大小的余弦值。
所成的銳二面角大小的余弦值。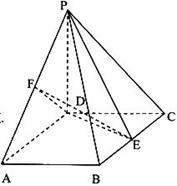
一、選擇題(每小題5分,滿分60分)
1
2
3
4
5
6
7
8
9
10
11
12
D
C
D
B
B
A
C
C
A
D
A
D
二、填空題(每小題4分,滿分16分)
13.-6 14. 15.
15. 16.②③
16.②③
三、解答題(第17、18、19、20、21題各12分,第22題14分,共74分)
17.(I)

(Ⅱ)



 函數
函數 的值域為
的值域為
18.解:(I)記“甲回答對這道題”、“乙回答對這道題”、“丙回答對這道題”分別為事件
 、
、 、
、 ,則
,則 ,且有
,且有 即
即

(Ⅱ)由(1)
則甲、乙、丙三人中恰有兩人回答對該題的概率為:

19.解:法一
(I)設 是
是 的中點,連結
的中點,連結 ,
,
則四邊形 為方形,
為方形, ,故
,故 ,
,

 即
即
又
 平面
平面
(Ⅱ)由(I)知 平面
平面 ,
,
又 平面
平面 ,
, ,
,
取 的中點
的中點 ,連結
,連結 又
又 ,
,
則 ,取
,取 的中點
的中點 ,連結
,連結 則
則
 為二面角
為二面角 的平面角
的平面角
連結 ,在
,在 中,
中, ,
,
取 的中點
的中點 ,連結
,連結 ,
, ,在
,在 中,
中,

 二面角
二面角 的余弦值為
的余弦值為
法二:
 (I)以
(I)以 為原點,
為原點, 所在直線分別為
所在直線分別為 軸,
軸, 軸,
軸, 軸建立如圖所示的空間直角坐標系,則
軸建立如圖所示的空間直角坐標系,則


又因為
所以, 平面
平面
(Ⅱ)設 為平面
為平面 的一個法向量。
的一個法向量。
由 得
得
取 ,則
,則 又
又 ,
,
設 為平面
為平面 的一個法向量,由
的一個法向量,由 ,
, ,
,
得 取
取 取
取
設 與
與 的夾角為
的夾角為 ,二面角
,二面角 為
為 ,顯然
,顯然 為銳角,
為銳角,
 ,即為所求
,即為所求
20.解:(I) 或
或
故 的單調遞增區間是
的單調遞增區間是 和
和
單調遞減區間是(0,2)
(Ⅱ)



 在
在 和
和 遞增,在(-1,3)遞減。
遞增,在(-1,3)遞減。
 有三個相異實根
有三個相異實根

21.解:(I)設 的公差為
的公差為 ,則:
,則:

(Ⅱ)當 時,
時, ,由
,由 ,得
,得
當 時,
時, ,
,
 ,即
,即
 是以
是以 為首項,
為首項, 為公比的等比數列。
為公比的等比數列。
(Ⅲ)由(Ⅱ)可知:


22.解:(I)設過 與拋物線
與拋物線 的相切的直線的斜率是
的相切的直線的斜率是 ,
,
則該切線的方程為:
由 得
得

則 都是方程
都是方程 的解,故
的解,故
(Ⅱ)設
由于 ,故切線
,故切線 的方程是:
的方程是:
則
 ,同理
,同理
則直線 的方程是
的方程是 ,則直線
,則直線 過定點(0,2)
過定點(0,2)
(Ⅲ)要使 最小,就是使得
最小,就是使得 到直線
到直線 的距離最小,而
的距離最小,而 到直線
到直線 的距離
的距離

當且僅當 即
即 時取等號
時取等號
設
由 得
得 ,則
,則



湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com