
題目列表(包括答案和解析)
設函數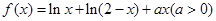 .
.
(Ⅰ) 當 時,求
時,求 的單調區間;
的單調區間;
(Ⅱ) 若 在
在 上的最大值為
上的最大值為 ,求
,求 的值.
的值.
【解析】第一問中利用函數 的定義域為(0,2),
的定義域為(0,2), .
.
當a=1時, 所以
所以 的單調遞增區間為(0,
的單調遞增區間為(0, ),單調遞減區間為(
),單調遞減區間為( ,2);
,2);
第二問中,利用當 時,
時, >0, 即
>0, 即 在
在 上單調遞增,故
上單調遞增,故 在
在 上的最大值為f(1)=a 因此a=1/2.
上的最大值為f(1)=a 因此a=1/2.
解:函數 的定義域為(0,2),
的定義域為(0,2), .
.
(1)當 時,
時, 所以
所以 的單調遞增區間為(0,
的單調遞增區間為(0, ),單調遞減區間為(
),單調遞減區間為( ,2);
,2);
(2)當 時,
時, >0, 即
>0, 即 在
在 上單調遞增,故
上單調遞增,故 在
在 上的最大值為f(1)=a 因此a=1/2.
上的最大值為f(1)=a 因此a=1/2.
給出下列四個命題:
①函數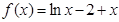 在區間
在區間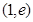 上存在零點;
上存在零點;
②若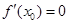 ,則函數
,則函數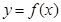 在
在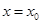 處取得極值;
處取得極值;
③若
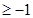 ,則函數
,則函數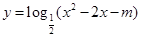 的值域為
的值域為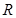 ;
;
④“ ”是“函數
”是“函數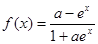 在定義域上是奇函數”的充分不必要條件。
在定義域上是奇函數”的充分不必要條件。
以上命題正確的是 (寫出所有正確命題的編號).
給出下列四個命題:
①函數 在區間
在區間 上存在零點;
上存在零點;
②若 ,則函數
,則函數 在
在 處取得極值;
處取得極值;
③若
 ,則函數
,則函數 的值域為
的值域為 ;
;
④“ ”是“函數
”是“函數 在定義域上是奇函數”的充分不必要條件。
在定義域上是奇函數”的充分不必要條件。
以上命題正確的是 (寫出所有正確命題的編號).
已知函數 .(
.( )
)
(1)若 在區間
在區間 上單調遞增,求實數
上單調遞增,求實數 的取值范圍;
的取值范圍;
(2)若在區間 上,函數
上,函數 的圖象恒在曲線
的圖象恒在曲線 下方,求
下方,求 的取值范圍.
的取值范圍.
【解析】第一問中,首先利用 在區間
在區間 上單調遞增,則
上單調遞增,則 在區間
在區間 上恒成立,然后分離參數法得到
上恒成立,然后分離參數法得到 ,進而得到范圍;第二問中,在區間
,進而得到范圍;第二問中,在區間 上,函數
上,函數 的圖象恒在曲線
的圖象恒在曲線 下方等價于
下方等價于 在區間
在區間 上恒成立.然后求解得到。
上恒成立.然后求解得到。
解:(1) 在區間
在區間 上單調遞增,
上單調遞增,
則 在區間
在區間 上恒成立. …………3分
上恒成立. …………3分
即 ,而當
,而當 時,
時, ,故
,故 .
…………5分
.
…………5分
所以 .
…………6分
.
…………6分
(2)令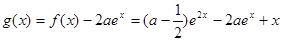 ,定義域為
,定義域為 .
.
在區間 上,函數
上,函數 的圖象恒在曲線
的圖象恒在曲線 下方等價于
下方等價于 在區間
在區間 上恒成立.
上恒成立.
∵ …………9分
…………9分
① 若 ,令
,令 ,得極值點
,得極值點 ,
, ,
,
當 ,即
,即 時,在(
時,在( ,+∞)上有
,+∞)上有 ,此時
,此時 在區間
在區間 上是增函數,并且在該區間上有
上是增函數,并且在該區間上有 ,不合題意;
,不合題意;
當 ,即
,即 時,同理可知,
時,同理可知, 在區間
在區間 上遞增,
上遞增,
有 ,也不合題意;
…………11分
,也不合題意;
…………11分
② 若 ,則有
,則有 ,此時在區間
,此時在區間 上恒有
上恒有 ,從而
,從而 在區間
在區間 上是減函數;
上是減函數;
要使 在此區間上恒成立,只須滿足
在此區間上恒成立,只須滿足
 ,
,
由此求得 的范圍是
的范圍是 . …………13分
. …………13分
綜合①②可知,當 時,函數
時,函數 的圖象恒在直線
的圖象恒在直線 下方.
下方.
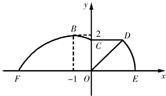 如圖,某市準備在道路EF的一側修建一條運動比賽道,賽道的前一部分為曲線段FBC,該曲線段是函數y=Asin(ωx+
如圖,某市準備在道路EF的一側修建一條運動比賽道,賽道的前一部分為曲線段FBC,該曲線段是函數y=Asin(ωx+| 2π |
| 3 |
| 3 |
 |
| DE |
 |
| DE |
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com