
題目列表(包括答案和解析)
已知函數(shù) 的定義域是
的定義域是 ,值域
,值域 ,則滿足條件的整數(shù)對(duì)
,則滿足條件的整數(shù)對(duì) 共有____對(duì)
共有____對(duì)
已知函數(shù)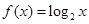 的定義域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012052601420391781618/SYS201205260142510428425523_ST.files/image002.png">,
的定義域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012052601420391781618/SYS201205260142510428425523_ST.files/image002.png">, ,且
,且 ,則滿足條件的函數(shù)
,則滿足條件的函數(shù) 的個(gè)數(shù)為( )
的個(gè)數(shù)為( )
A.
1 B. 1023 C. 1024 D. 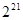
已知函數(shù) 的定義域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012040912520459371212/SYS201204091252267656313883_ST.files/image002.gif">,
的定義域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012040912520459371212/SYS201204091252267656313883_ST.files/image002.gif">, ,且
,且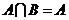 ,則滿足條件的函數(shù)
,則滿足條件的函數(shù) 的個(gè)數(shù)為 ( )
的個(gè)數(shù)為 ( )
A.1
B.1023 C.1024 D.
| A、f(x)=x2+ln|x| | B、f(x)=x2-ln|x| | C、f(x)=x+ln|x| | D、f(x)=x-ln|x| |
一、選擇題
D A A C D C D C B B
二、填空題:
11. 年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image239.gif) 12.
12.年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image241.gif) 13.81 14.
13.81 14.年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image243.gif) 15.②③
15.②③
三、解答題:
16.解:把函數(shù)年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image245.gif) 按向量
按向量年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image171.gif)
年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image173.gif) 平移后得
平移后得年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image248.gif) ..............2分
..............2分
(Ⅰ)年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image176.gif) =
=年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image250.gif) ..................3分
..................3分
年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image252.gif) ............5分
............5分
則函數(shù)年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image176.gif) 的值域?yàn)?sub>
的值域?yàn)?sub>年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image254.gif) ;.....................7分
;.....................7分
(Ⅱ)當(dāng)年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image178.gif) 時(shí),
時(shí),年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image257.gif) ,
,年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image259.gif)
年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image261.gif) .............................................9分
.............................................9分
年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image263.gif) 恒有解,
恒有解,年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image265.gif) ,..................................11分
,..................................11分
即年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image267.gif) ....................................................12分
....................................................12分
17.解:(Ⅰ)設(shè)三角形三內(nèi)角A、B、C對(duì)應(yīng)的三邊分別為a, b, c,
∵年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image269.gif) ,∴
,∴年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image271.gif) ,由正弦定理有
,由正弦定理有年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image273.gif) ,
,
又由余弦定理有年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image275.gif) ,∴
,∴年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image277.gif) ,即
,即年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image279.gif) ,
,
所以年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image280.gif) 為Rt
為Rt年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image280.gif) ,且
,且年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image282.gif) .................................. 3分
.................................. 3分
又年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image284.gif)
年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image286.gif)
(1)÷(2),得年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image288.gif) ...................................... 4分
...................................... 4分
令a=4k, b=3k (k>0)
則年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image290.gif) ∴三邊長(zhǎng)分別為3,4,5.....................6分
∴三邊長(zhǎng)分別為3,4,5.....................6分
(Ⅱ)以C為坐標(biāo)原點(diǎn),射線CA為x軸正半軸建立直角坐標(biāo)系,則A、B坐標(biāo)為(3,0),(0,4),直線AB方程為年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image292.gif)
設(shè)P點(diǎn)坐標(biāo)為(x, y),則由P到三邊AB、BC、AB的距離為d1, d2和d3可知
年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image294.gif) ,..................................8分
,..................................8分
且年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image296.gif) 故
故年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image298.gif) .......................10分
.......................10分
令年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image300.gif) ,由線性規(guī)劃知識(shí)可知0≤m≤8,故d1+d2+d3的取值范圍是
,由線性規(guī)劃知識(shí)可知0≤m≤8,故d1+d2+d3的取值范圍是年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image302.gif) ......12分
......12分
18.解:(Ⅰ)當(dāng)年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image304.gif)
年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image306.gif) ………………2分
………………2分
年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image308.gif)
年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image310.gif) ,..............................................5分
,..............................................5分
故年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image312.gif) ................6分
................6分
定義域?yàn)?sub>年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image314.gif) .................................7分
.................................7分
(Ⅱ)對(duì)于年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image316.gif) ,
,
顯然當(dāng)年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image318.gif) (元), ..................................9分
(元), ..................................9分
年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image320.gif)
∴當(dāng)每輛自行車的日租金定在11元時(shí),才能使一日的凈收入最多。..........12分
19.解: (Ⅰ) ∵年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image322.gif) (1)=0
(1)=0
∴(an+2-an+1)-(
即an+2-2an+1=2(an+1-2an)
又a2-
∴數(shù)列{an+1-2an}是以2為公比,以4為首項(xiàng)的等比數(shù)列。...............2分
∴an+1-2an=4×2n-1=2 n+1
∴年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image324.gif) 且
且年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image326.gif)
∴數(shù)列{年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image328.gif) }是首項(xiàng)為1,公差為1的等差數(shù)列,....................4分
}是首項(xiàng)為1,公差為1的等差數(shù)列,....................4分
∴年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image328.gif) =
=年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image330.gif) +(n-1)×1=n
+(n-1)×1=n
∴年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image332.gif) .....................................................6分
.....................................................6分
(Ⅱ)由年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image334.gif) ,
,年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image336.gif)
令Sn=|b1|+|b2|+…+|bn|=+2()2+3()3+…+n()n
Sn=()2+2()3+…+(n-1)()n+n()n+1.......................8分
得Sn=+()2+()3+…+()n-n()n+1
=-n()n+1=2[1-()n]-n()n+1
∴ Sn=6[1-()n]-3n()n+1<年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image338.gif) .....................10分
.....................10分
要使得|b1|+|b2|+…+|bn|<m對(duì)于n∈N*恒成立,只須年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image340.gif)
所以實(shí)數(shù)年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image217.gif) 的取值范圍是
的取值范圍是年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image340.gif) 。.......................................12分
。.......................................12分
20.解:(Ⅰ)因?yàn)?sub>年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image344.gif)
又年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image221.gif) 是函數(shù)
是函數(shù)年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image099.gif) 的極值點(diǎn),
的極值點(diǎn),年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image346.gif) ,即
,即年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image348.gif) ..............2分
..............2分
年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image350.gif) ,則
,則年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image352.gif)
年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image284.gif) ............4分
............4分
年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image354.gif) .........................................................6分
.........................................................6分
(Ⅱ)由(Ⅰ)可知年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image356.gif)
故年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image358.gif) .................................8分
.................................8分
令年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image360.gif) ,當(dāng)
,當(dāng)年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image362.gif) 時(shí),得
時(shí),得年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image364.gif) ,
,
則當(dāng)年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image366.gif) 時(shí),
時(shí),年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image368.gif) ;當(dāng)
;當(dāng)年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image370.gif) 時(shí),
時(shí),年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image372.gif) ,
,
所以年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image374.gif) 在
在年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image366.gif) 上單調(diào)遞減,在
上單調(diào)遞減,在年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image370.gif) 單調(diào)遞增,..................10分
單調(diào)遞增,..................10分
故年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image376.gif) 時(shí),
時(shí),年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image378.gif) ,又
,又年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image380.gif) ,..................................12分
,..................................12分
即對(duì)任意年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image382.gif) ,恒有
,恒有年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image233.gif) 。..................................13分
。..................................13分
21.解:(Ⅰ) 以AB所在直線為x軸,線段AB的中垂線為y軸建立直角坐標(biāo)系,
設(shè) |CA|+|CB|=
所以焦距
因?yàn)?年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image384.gif)
又 年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image386.gif) ,所以
,所以 年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image388.gif) ,
,
由題意得 年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image390.gif) ...........................................4分
...........................................4分
此時(shí),|PA|=|PB|,P點(diǎn)坐標(biāo)為 P(0,±4).
所以C點(diǎn)的軌跡方程為 年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image392.gif) .............................6分
.............................6分
(Ⅱ)不妨設(shè)A點(diǎn)坐標(biāo)為A(-3,0),M(x1,y1),N(x2,y2)
(1)當(dāng)直線MN的傾斜角不為900時(shí),設(shè)其方程為 y=k(x+3) 代入橢圓方程化簡(jiǎn),得
年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image394.gif) .......................................7分
.......................................7分
顯然有
△≥0, 所以 年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image396.gif)
而由橢圓第二定義可得
年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image398.gif)
......................... 10分
只要考慮
年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image400.gif) 的最小值,即考慮
的最小值,即考慮年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image402.gif) 取最小值,顯然.
取最小值,顯然.
當(dāng)k=0時(shí),年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image237.gif) 取最小值16. .................................12分
取最小值16. .................................12分
(2)當(dāng)直線MN的傾斜角為900時(shí),x1=x2=-3,得
年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image405.gif) .....12分
.....12分
但 年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image392.gif) ,故
,故年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image407.gif) ,這樣的M、N不存在,即
,這樣的M、N不存在,即年度湖北補(bǔ)習(xí)學(xué)校聯(lián)合體大聯(lián)考-數(shù)學(xué)理.files/image237.gif) 的最小值的集合為空集............................................................14分
的最小值的集合為空集............................................................14分
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com