
題目列表(包括答案和解析)
本題有(1)、(2)、(3)三個選答題,每小題7分,請考生任選2題作答,滿分14分,如果多做,則按所做的前兩題計分.作答時,先用2B鉛筆在答題卡上把所選題目對應的題號涂黑,并將所選題號填入括號中.
(1)(本小題滿分7分)選修4-2:矩陣與變換
已知矩陣 ,向量
,向量 .
.
(I)求矩陣 的特征值
的特征值 、
、 和特征向量
和特征向量 ;
;
(II)求 的值.
的值.
(2)(本小題滿分7分)選修4-4:坐標系與參數方程
在平面直角坐標系xOy中,已知曲線C的參數方程為 .以直角坐標系原點O為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標方程為
.以直角坐標系原點O為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標方程為 .
.
(Ⅰ)求直線l的直角坐標方程;
(Ⅱ)點P為曲線C上的動點,求點P到直線l距離的最大值.
(3)(本小題滿分7分)選修4-5:不等式選講
(Ⅰ)已知:a、b、 ;w.w.w.k.s.5.u.c.o.m
;w.w.w.k.s.5.u.c.o.m
(Ⅱ)某長方體從一個頂點出發的三條棱長之和等于3,求其對角線長的最小值.
某工廠對一批產品進行了抽樣檢測.右圖是根據抽樣檢測后的w.w.w.k.s.5.u.c.o.m ![]()
![]()
產品凈重(單位:克)數據繪制的頻率分布直方圖,其中產品
凈重的范圍是[96,106],樣本數據分組為[96,98),[98,100),
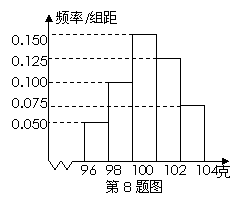 [100,102),[102,104),[104,106],已知樣本中產品凈重小于
[100,102),[102,104),[104,106],已知樣本中產品凈重小于
100克的個數是36,則樣本中凈重大于或等于98克并且
小于104克的產品的個數是( ).
A.90 B.75 C. 60 D.45
已知等差數列![]() 的公差為2,若
的公差為2,若![]() 成等比數列, 則
成等比數列, 則![]() 等于w.w.w.k.s.5.u.c.o.m
等于w.w.w.k.s.5.u.c.o.m ![]()
![]()
A.4 B.6 C.8 D.10
已知雙曲線![]() 的右焦點為
的右焦點為![]() ,過
,過![]() 且斜率為
且斜率為![]() 的直線交
的直線交![]() 于
于![]() 兩點,若
兩點,若![]() ,則
,則![]() 的離心率為w.w.w.k.s.5.u.c.o.
的離心率為w.w.w.k.s.5.u.c.o.
m A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
(8) 已知函數![]() =Acos(
=Acos(![]() )的圖象如圖所示,
)的圖象如圖所示,![]() ,則
,則![]() =
=

(A)![]() (B)
(B) ![]() (C)-
(C)- ![]() (D)
(D) ![]() w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
![]()
1-8 BACBD BDD
9..files/image248.gif) 10. 400 11.
10. 400 11. .files/image250.gif) 12. 128 13..
12. 128 13.. .files/image252.gif)
.files/image254.gif) 14.
14..files/image256.gif) 15.
15..files/image258.gif)
解析:5.數形結合法 7.解:由圖知三角形ABC為等腰三角形,只要∠AF2B為銳角即可,所以有.files/image260.gif) ,即
,即.files/image262.gif) ,解出
,解出.files/image264.gif)
.files/image099.gif) ,故選D
,故選D
8.由已知得.files/image214.gif) 圖關于
圖關于.files/image193.gif) 軸對稱,且
軸對稱,且.files/image214.gif) 的周期是2,所以可作出
的周期是2,所以可作出.files/image214.gif) 在[-1,1]的圖象,由圖的單增性結合三角函數值可判斷D。
在[-1,1]的圖象,由圖的單增性結合三角函數值可判斷D。
12.解:當.files/image269.gif) 時,
時,.files/image271.gif) ,相減得
,相減得.files/image273.gif) ,且由已知得
,且由已知得.files/image275.gif) ,所以所求為
,所以所求為.files/image277.gif) 14,因為
14,因為.files/image279.gif) 由題意得
由題意得.files/image281.gif) ,解得
,解得.files/image283.gif)
.files/image256.gif)
15,解:由題知△BED~△BCE,所以.files/image285.gif) ,可求得BE=
,可求得BE=.files/image258.gif)
16.解:(Ⅰ)由題意得.files/image287.gif)
由A為銳角得.files/image289.gif) ,
,.files/image291.gif)
(Ⅱ)由(Ⅰ)知.files/image293.gif) ,所以
,所以.files/image295.gif)
.files/image297.gif)
因為.files/image299.gif) ,所以
,所以.files/image301.gif) ,因此,當
,因此,當.files/image303.gif) 時,
時,.files/image305.gif) 有最大值
有最大值.files/image307.gif) ,
,
當.files/image309.gif) 時,
時,.files/image305.gif) 有最小值 ? 3,所以所求函數
有最小值 ? 3,所以所求函數.files/image305.gif) 的值域是
的值域是.files/image313.gif)
17.解:令.files/image315.gif) 分別表示甲、乙、丙在第k局中獲勝.
分別表示甲、乙、丙在第k局中獲勝.
(Ⅰ)由獨立事件同時發生與互斥事件至少有一個發生的概率公式知,打滿3局比賽還未停止的概率為.files/image317.gif)
(Ⅱ).files/image319.gif) 的所有可能值為2,3,4,5,6,且
的所有可能值為2,3,4,5,6,且.files/image321.gif)
.files/image323.gif)
.files/image325.gif)
.files/image327.gif)
.files/image329.gif)
故有分布列
.files/image331.gif)
.files/image319.gif)
2
3
4
5
6
P
.files/image195.gif)
.files/image019.gif)
.files/image336.gif)
.files/image338.gif)
.files/image338.gif)
從而.files/image341.gif) (局).
(局).
18.證(1)因為.files/image170.gif) 側面
側面.files/image172.gif) ,故
,故.files/image343.gif)
.files/image039.jpg)
在.files/image345.gif) 中,
中,.files/image347.gif) 由余弦定理有
由余弦定理有 .files/image039.jpg)
.files/image349.gif)
.files/image039.jpg)
.files/image351.gif) 故有
故有
.files/image353.gif)
.files/image039.jpg)
而.files/image355.gif) 且
且.files/image357.gif) 平面
平面.files/image359.gif)
.files/image039.jpg)
.files/image361.gif)
.files/image176.gif)
.files/image039.jpg)
.files/image039.jpg) (2)
(2).files/image363.gif)
.files/image039.jpg)
從而.files/image365.gif) 且
且.files/image367.gif) 故
故.files/image369.gif)
.files/image039.jpg)
不妨設 .files/image371.gif) ,則
,則.files/image373.gif) ,則
,則.files/image375.gif)
.files/image039.jpg)
又.files/image377.gif) 則
則.files/image379.gif)
.files/image039.jpg)
在.files/image381.gif) 中有
中有
.files/image383.gif) 從而
從而.files/image385.gif) (舍負)
(舍負).files/image039.jpg)
故.files/image148.gif) 為
為.files/image178.gif) 的中點時,
的中點時,.files/image183.gif)
.files/image039.jpg)
(3)取.files/image387.gif) 的中點
的中點.files/image389.gif) ,
,.files/image391.gif) 的中點
的中點.files/image393.gif) ,
,.files/image395.gif) 的中點
的中點.files/image397.gif) ,
,.files/image399.gif) 的中點
的中點.files/image200.gif)
.files/image039.jpg)
.files/image402.gif) 連
連.files/image404.gif) 則
則.files/image406.gif) ,連
,連.files/image408.gif) 則
則.files/image410.gif) ,連
,連.files/image412.gif) 則
則.files/image414.gif)
.files/image039.jpg)
連.files/image416.gif) 則
則.files/image418.gif) ,且
,且.files/image420.gif) 為矩形,
為矩形,.files/image422.gif)
.files/image039.jpg)
又.files/image424.gif) 故
故.files/image426.gif) 為所求二面角的平面角
為所求二面角的平面角.files/image039.jpg)
在.files/image428.gif) 中,
中,.files/image430.gif)
.files/image432.gif)
.files/image434.gif)
19.解:(1)依題意,.files/image197.gif) 到
到.files/image191.gif) 距離等于
距離等于.files/image197.gif) 到直線
到直線.files/image439.gif) 的距離,曲線
的距離,曲線.files/image144.gif) 是以原點為頂點,
是以原點為頂點,.files/image191.gif) 為焦點的拋物線
為焦點的拋物線 .files/image443.gif) 曲線
曲線.files/image144.gif) 方程是
方程是.files/image445.gif)
(2)設圓心.files/image447.gif) ,因為圓
,因為圓.files/image200.gif) 過
過.files/image202.gif)
故設圓的方程.files/image451.gif) 令
令.files/image453.gif) 得:
得:.files/image455.gif)
設圓與.files/image193.gif) 軸的兩交點為
軸的兩交點為.files/image458.gif) ,則
,則.files/image460.gif)
.files/image462.gif)
.files/image447.gif) 在拋物線
在拋物線.files/image445.gif) 上,
上,.files/image466.gif)
.files/image468.gif)
.files/image470.gif)
所以,當.files/image200.gif) 運動時,弦長
運動時,弦長.files/image208.gif) 為定值2
為定值2
20.解:(1).files/image474.gif) ,依題意有
,依題意有.files/image476.gif) ,故
,故.files/image478.gif) .
.
從而.files/image480.gif) .
.
.files/image214.gif) 的定義域為
的定義域為.files/image483.gif) ,當
,當.files/image485.gif) 時,
時,.files/image487.gif) ;
;
當.files/image489.gif) 時,
時,.files/image491.gif) ;當
;當.files/image493.gif) 時,
時,.files/image487.gif) .
.
從而,.files/image214.gif) 分別在區間
分別在區間.files/image496.gif) 單調增加,在區間
單調增加,在區間.files/image498.gif) 單調減少.
單調減少.
(2).files/image214.gif) 的定義域為
的定義域為.files/image501.gif) ,
,.files/image503.gif) .
.
方程.files/image505.gif) 的判別式
的判別式.files/image507.gif) .
.
①若.files/image509.gif) ,即
,即.files/image511.gif) ,在
,在.files/image214.gif) 的定義域內
的定義域內.files/image487.gif) ,故
,故.files/image214.gif) 無極值.
無極值.
②若.files/image516.gif) ,則
,則.files/image518.gif) 或
或.files/image520.gif) .若
.若.files/image518.gif) ,
,.files/image522.gif) ,
,.files/image524.gif) .
.
當.files/image526.gif) 時,
時,.files/image528.gif) ,當
,當.files/image530.gif) 時,
時,.files/image487.gif) ,所以
,所以.files/image214.gif) 無極值.若
無極值.若.files/image520.gif) ,
,.files/image534.gif) ,
,.files/image536.gif) ,
,.files/image214.gif) 也無極值.
也無極值.
③若.files/image539.gif) ,即
,即.files/image541.gif) 或
或.files/image543.gif) ,則
,則.files/image505.gif) 有兩個不同的實根
有兩個不同的實根.files/image546.gif) ,
,.files/image548.gif) .
.
當.files/image543.gif) 時,
時,.files/image551.gif) ,從而
,從而.files/image553.gif) 有
有.files/image214.gif) 的定義域內沒有零點,故
的定義域內沒有零點,故.files/image214.gif) 無極值.
無極值.
當.files/image541.gif) 時,
時,.files/image558.gif) ,
,.files/image560.gif) ,
,.files/image553.gif) 在
在.files/image214.gif) 的定義域內有兩個不同的零點,由根值判別方法知
的定義域內有兩個不同的零點,由根值判別方法知.files/image214.gif) 在
在.files/image565.gif) 取得極值.綜上,
取得極值.綜上,.files/image214.gif) 存在極值時,
存在極值時,.files/image115.gif) 的取值范圍為
的取值范圍為.files/image569.gif) .
..files/image214.gif) 的極值之和為
的極值之和為
.files/image572.gif) .
.
.files/image574.jpg) 21.解:(1)由點P
21.解:(1)由點P.files/image576.gif) 在直線
在直線.files/image228.gif) 上,即
上,即.files/image579.gif) ,且
,且.files/image581.gif) ,數列{
,數列{.files/image583.gif) }
}
是以1為首項,1為公差的等差數列
.files/image585.gif) ,
,.files/image581.gif) 同樣滿足,所以
同樣滿足,所以.files/image587.gif)
(2).files/image589.gif)
.files/image591.gif)
.files/image593.gif)
所以.files/image234.gif) 是單調遞增,故
是單調遞增,故.files/image234.gif) 的最小值是
的最小值是.files/image597.gif)
.files/image598.jpg) (3)
(3).files/image600.gif) ,可得
,可得.files/image602.gif) ,
,.files/image604.gif)
.files/image606.gif) ,
,
.files/image608.gif)
……
.files/image610.gif)
.files/image612.gif)
.files/image614.gif) ,n≥2
,n≥2
.files/image616.gif)
故存在關于n的整式g(x)=n,使得對于一切不小于2的自然數n恒成立.
(2)法二:以.files/image089.gif) 為原點
為原點.files/image619.gif) 為
為.files/image621.gif) 軸,設
軸,設.files/image371.gif) ,則
,則
.files/image624.gif) 由
由.files/image183.gif) 得
得 .files/image627.gif) 即
即.files/image039.jpg)
.files/image629.gif)
.files/image631.gif)
.files/image039.jpg)
化簡整理得 .files/image633.gif) ,
,.files/image635.gif) 或
或 .files/image637.gif)
.files/image039.jpg)
當.files/image637.gif) 時
時.files/image148.gif) 與
與.files/image639.gif) 重合不滿足題意
重合不滿足題意.files/image039.jpg)
當.files/image635.gif) 時
時.files/image148.gif) 為
為.files/image178.gif) 的中點
的中點.files/image039.jpg)
故.files/image148.gif) 為
為.files/image178.gif) 的中點使
的中點使.files/image183.gif)
.files/image039.jpg)
(3)法二:由已知.files/image641.gif) ,
所以二面角
,
所以二面角.files/image185.gif) 的平面角
的平面角.files/image643.gif) 的大小為向量
的大小為向量.files/image645.gif) 與
與.files/image647.gif) 的夾角 因為
的夾角 因為.files/image649.gif)
.files/image651.gif)
故 
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com