
題目列表(包括答案和解析)
已知數列 滿足
滿足 (I)求數列
(I)求數列 的通項公式;
的通項公式;
(II)若數列 中
中 ,前
,前 項和為
項和為 ,且
,且 證明:
證明:
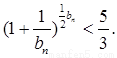
【解析】第一問中,利用 ,
,
∴數列{ }是以首項a1+1,公比為2的等比數列,即
}是以首項a1+1,公比為2的等比數列,即
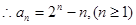
第二問中,

進一步得到得 即
即
即 是等差數列.
是等差數列.
然后結合公式求解。
解:(I) 解法二、 ,
,
∴數列{ }是以首項a1+1,公比為2的等比數列,即
}是以首項a1+1,公比為2的等比數列,即
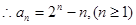
(II)
 ………②
………②
由②可得: …………③
…………③
③-②,得 即
即 …………④
…………④
又由④可得 …………⑤
…………⑤
⑤-④得
即 是等差數列.
是等差數列.


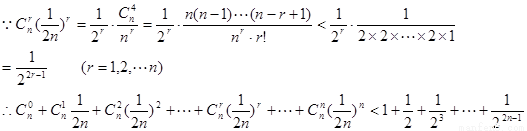


已知函數 ,數列
,數列 的項滿足:
的項滿足: ,(1)試求
,(1)試求
(2) 猜想數列 的通項,并利用數學歸納法證明.
的通項,并利用數學歸納法證明.
【解析】第一問中,利用遞推關系 ,
, 
 ,
, 
第二問中,由(1)猜想得: 然后再用數學歸納法分為兩步驟證明即可。
然后再用數學歸納法分為兩步驟證明即可。
解: (1)  ,
,

 ,
,  …………….7分
…………….7分
(2)由(1)猜想得:
(數學歸納法證明)i)  ,
,
 ,命題成立
,命題成立
ii) 假設 時,
時, 成立
成立
則 時,
時,


綜合i),ii) :  成立
成立
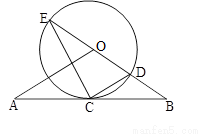
如圖,直線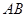 經過⊙
經過⊙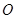 上的點
上的點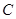 ,并且
,并且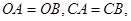 ⊙
⊙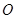 交直線
交直線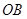 于
于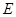 ,
,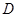 ,連接
,連接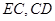 .
.
(I)求證:直線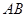 是⊙
是⊙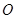 的切線;
的切線;
(II)若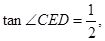 ⊙
⊙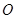 的半徑為
的半徑為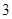 ,求
,求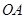 的長.
的長.
【解析】(1)證明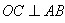 ;(II)根據
;(II)根據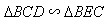 ,
,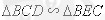
兩次相似求得。
過拋物線

 的對稱軸上的定點
的對稱軸上的定點 ,作直線
,作直線 與拋物線相交于
與拋物線相交于 兩點.
兩點.
(I)試證明 兩點的縱坐標之積為定值;
兩點的縱坐標之積為定值;
(II)若點 是定直線
是定直線 上的任一點,試探索三條直線
上的任一點,試探索三條直線 的斜率之間的關系,并給出證明.
的斜率之間的關系,并給出證明.
【解析】本題主要考查拋物線與直線的位置關系以及發現問題和解決問題的能力.
(1)中證明:設 下證之:設直線AB的方程為: x=ty+m與y2=2px聯立得消去x得y2=2pty-2pm=0,由韋達定理得
下證之:設直線AB的方程為: x=ty+m與y2=2px聯立得消去x得y2=2pty-2pm=0,由韋達定理得

(2)中:因為三條直線AN,MN,BN的斜率成等差數列,下證之
設點N(-m,n),則直線AN的斜率KAN= ,直線BN的斜率KBN=
,直線BN的斜率KBN=

KAN+KBN= +
+
本題主要考查拋物線與直線的位置關系以及發現問題和解決問題的能力.
零件直徑相等的概率。本小題主要考查用列舉法計算隨機事件所含的基本事件數及事件發生的概率等基礎知識,考查數據處理能力及運用概率知識解決簡單的實際問題的能力。滿分12分
【解析】(Ⅰ)解:由所給數據可知,一等品零件共有6個.設“從10個零件中,隨機抽取一個為一等品”為事件A,則P(A)=![]() =
=![]() .
.
(Ⅱ)(i)解:一等品零件的編號為![]() .從這6個一等品零件中隨機抽取2個,所有可能的結果有:
.從這6個一等品零件中隨機抽取2個,所有可能的結果有:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() 共有15種.
共有15種.
(ii)解:“從一等品零件中,隨機抽取的2個零件直徑相等”(記為事件B)的所有可能結果有:![]() ,
,![]() ,共有6種.
,共有6種.
所以P(B)=![]() .
.
(本小題滿分12分)
如圖,在五面體ABCDEF中,四邊形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=![]() ,∠BAD=∠CDA=45°.
,∠BAD=∠CDA=45°.
 (Ⅰ)求異面直線CE與AF所成角的余弦值;
(Ⅰ)求異面直線CE與AF所成角的余弦值;
(Ⅱ)證明CD⊥平面ABF;
(Ⅲ)求二面角B-EF-A的正切值。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com