
題目列表(包括答案和解析)
設(shè)橢圓 的左、右頂點(diǎn)分別為
的左、右頂點(diǎn)分別為 ,點(diǎn)
,點(diǎn) 在橢圓上且異于
在橢圓上且異于 兩點(diǎn),
兩點(diǎn), 為坐標(biāo)原點(diǎn).
為坐標(biāo)原點(diǎn).
(Ⅰ)若直線(xiàn) 與
與 的斜率之積為
的斜率之積為 ,求橢圓的離心率;
,求橢圓的離心率;
(Ⅱ)若 ,證明直線(xiàn)
,證明直線(xiàn) 的斜率
的斜率
 滿(mǎn)足
滿(mǎn)足
【解析】(1)解:設(shè)點(diǎn)P的坐標(biāo)為 .由題意,有
.由題意,有 ①
①
由 ,得
,得 ,
,
由 ,可得
,可得 ,代入①并整理得
,代入①并整理得
由于 ,故
,故 .于是
.于是 ,所以橢圓的離心率
,所以橢圓的離心率
(2)證明:(方法一)
依題意,直線(xiàn)OP的方程為 ,設(shè)點(diǎn)P的坐標(biāo)為
,設(shè)點(diǎn)P的坐標(biāo)為 .
.
由條件得 消去
消去 并整理得
并整理得 ②
②
由 ,
, 及
及 ,
,
得 .
.
整理得 .而
.而 ,于是
,于是 ,代入②,
,代入②,
整理得
由 ,故
,故 ,因此
,因此 .
.
所以 .
.
(方法二)
依題意,直線(xiàn)OP的方程為 ,設(shè)點(diǎn)P的坐標(biāo)為
,設(shè)點(diǎn)P的坐標(biāo)為 .
.
由P在橢圓上,有
因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012071821180638818491/SYS201207182118494193384555_ST.files/image036.png">, ,所以
,所以 ,即
,即 ③
③
由 ,
, ,得
,得 整理得
整理得 .
.
于是 ,代入③,
,代入③,
整理得
解得 ,
,
所以 .
.
(08年杭州市質(zhì)檢二)(14分)如圖,在橢圓![]() 中,點(diǎn)
中,點(diǎn)![]() 是左焦點(diǎn),
是左焦點(diǎn), ![]() ,
,![]() 分別為右頂點(diǎn)和上頂點(diǎn),點(diǎn)
分別為右頂點(diǎn)和上頂點(diǎn),點(diǎn)![]() 為橢圓的中心。又點(diǎn)
為橢圓的中心。又點(diǎn)![]() 在橢圓上,且滿(mǎn)足條件:
在橢圓上,且滿(mǎn)足條件:![]() ,點(diǎn)
,點(diǎn)![]() 是點(diǎn)
是點(diǎn)![]() 在x軸上的射影。
在x軸上的射影。
(1)求證:當(dāng)![]() 取定值時(shí),點(diǎn)
取定值時(shí),點(diǎn)![]() 必為定點(diǎn);
必為定點(diǎn);
(2)如果點(diǎn)![]() 落在左頂點(diǎn)與左焦點(diǎn)之間,試求橢圓離心率的取值范圍;
落在左頂點(diǎn)與左焦點(diǎn)之間,試求橢圓離心率的取值范圍;
(3)如果以![]() 為直徑的圓與直線(xiàn)
為直徑的圓與直線(xiàn)![]() 相切,且凸四邊形
相切,且凸四邊形![]() 的面積等于
的面積等于![]() ,求橢圓的方程。
,求橢圓的方程。
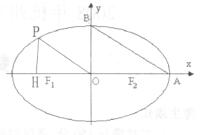
已知橢圓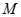 的對(duì)稱(chēng)軸為坐標(biāo)軸,焦點(diǎn)是(0,
的對(duì)稱(chēng)軸為坐標(biāo)軸,焦點(diǎn)是(0, ),(0,
),(0,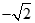 ),又點(diǎn)
),又點(diǎn)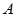
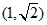 在橢圓
在橢圓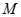 上.
上.
(1)求橢圓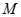 的方程;
的方程;
(2)已知直線(xiàn)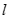 的斜率為
的斜率為 ,若直線(xiàn)
,若直線(xiàn)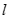 與橢圓
與橢圓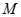 交于
交于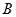 、
、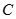 兩點(diǎn),求
兩點(diǎn),求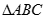 面積的最大值.
面積的最大值.
2.A解析:由![]() 知函數(shù)在
知函數(shù)在![]() 上有零點(diǎn),又因?yàn)楹瘮?shù)在(0,+
上有零點(diǎn),又因?yàn)楹瘮?shù)在(0,+![]() )上是減函數(shù),所以函數(shù)y=f(x) 在(0,+
)上是減函數(shù),所以函數(shù)y=f(x) 在(0,+![]() )上有且只有一個(gè)零點(diǎn)不妨設(shè)為
)上有且只有一個(gè)零點(diǎn)不妨設(shè)為![]() ,則
,則![]() ,又因?yàn)楹瘮?shù)是偶函數(shù),所以
,又因?yàn)楹瘮?shù)是偶函數(shù),所以![]() =0并且函數(shù)在(0,+
=0并且函數(shù)在(0,+![]() )上是減函數(shù),因此-
)上是減函數(shù),因此-![]() 是(-
是(-![]() ,0)上的唯一零點(diǎn),所以函數(shù)共有兩個(gè)零點(diǎn)
,0)上的唯一零點(diǎn),所以函數(shù)共有兩個(gè)零點(diǎn)
下列敘述中,是隨機(jī)變量的有( )
①某工廠(chǎng)加工的零件,實(shí)際尺寸與規(guī)定尺寸之差;②標(biāo)準(zhǔn)狀態(tài)下,水沸騰的溫度;③某大橋一天經(jīng)過(guò)的車(chē)輛數(shù);④向平面上投擲一點(diǎn),此點(diǎn)坐標(biāo).
A.②③ B.①② C.①③④ D.①③
(09年?yáng)|城區(qū)期末理)(13分)
已知橢圓![]() 的對(duì)稱(chēng)軸為坐標(biāo)軸,且拋物線(xiàn)
的對(duì)稱(chēng)軸為坐標(biāo)軸,且拋物線(xiàn)![]() 的焦點(diǎn)是橢圓
的焦點(diǎn)是橢圓![]() 的一個(gè)焦點(diǎn),又點(diǎn)
的一個(gè)焦點(diǎn),又點(diǎn)![]()
![]() 在橢圓
在橢圓![]() 上.
上.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)已知直線(xiàn)![]() 的方向向量為
的方向向量為![]() ,若直線(xiàn)
,若直線(xiàn)![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點(diǎn),求
兩點(diǎn),求![]() 面積的最大值.
面積的最大值.
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com