
題目列表(包括答案和解析)
選答題(本小題滿分10分)(請考生在第22、23、24三道題中任選一題做答,并用2B鉛筆在答題卡上把所選題目的題號涂黑。注意所做題號必須與所涂題目的題號一致,并在答題卡指定區(qū)域答題。如果多做,則按所做的第一題計分。)
22.選修4-1:幾何證明選講
如圖,已知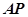 是⊙
是⊙ 的切線,
的切線,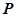 為切點,
為切點,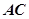 是⊙
是⊙ 的割線,與⊙
的割線,與⊙ 交于
交于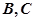 兩點,圓心
兩點,圓心 在
在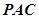 的內部,點
的內部,點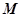 是
是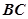 的中點。
的中點。
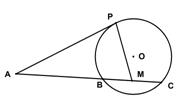
(1)證明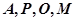 四點共圓;
四點共圓;
(2)求 的大小。
的大小。
23.選修4—4:坐標系與參數(shù)方程[來源:ZXXK]
已知直線 經(jīng)過點
經(jīng)過點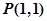 ,傾斜角
,傾斜角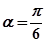 。
。
(1)寫出直線 的參數(shù)方程;
的參數(shù)方程;
(2)設 與曲線
與曲線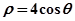 相交于兩點
相交于兩點 ,求點
,求點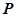 到
到 兩點的距離之積。
兩點的距離之積。
24.選修4—5:不等式證明選講
若不等式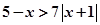 與不等式
與不等式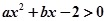 同解,而
同解,而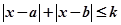 的解集為空集,求實數(shù)
的解集為空集,求實數(shù)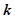 的取值范圍。
的取值范圍。
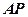 是⊙
是⊙ 的切線,
的切線,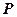 為切點,
為切點,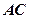 是⊙
是⊙ 的割線,與⊙
的割線,與⊙ 交于
交于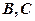 兩點,圓心
兩點,圓心 在
在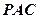 的內部,點
的內部,點
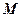 是
是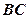 的中點。
的中點。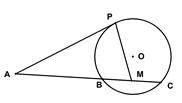
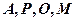 四點共圓;
四點共圓;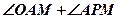 的大小。
的大小。 經(jīng)過點
經(jīng)過點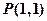 ,傾斜角
,傾斜角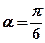 。
。 的參數(shù)方程;
的參數(shù)方程; 與曲線
與曲線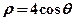 相交于兩點
相交于兩點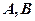 ,求點
,求點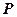 到
到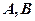 兩點的距離之積。
兩點的距離之積。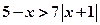 與不等式
與不等式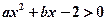 同解,而
同解,而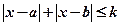 的解集為空集,求實數(shù)
的解集為空集,求實數(shù)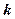 的取值范圍。
的取值范圍。選答題(本小題滿分10分)(請考生在第22、23、24三道題中任選一題做答,并用2B鉛筆在答題卡上把所選題目的題號涂黑。注意所做題號必須與所涂題目的題號一致,并在答題卡指定區(qū)域答題。如果多做,則按所做的第一題計分。)
22.選修4-1:幾何證明選講
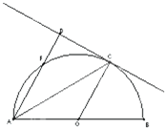
如圖,已知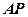 是⊙
是⊙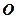 的切線,
的切線,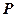 為切點,
為切點,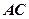 是⊙
是⊙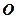 的割線,與⊙
的割線,與⊙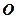 交于
交于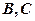 兩點,圓心
兩點,圓心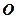 在
在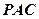 的內部,點
的內部,點
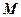 是
是 的中點。
的中點。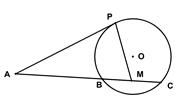
(1)證明 四點共圓;
四點共圓;
(2)求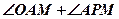 的大小。
的大小。
23.選修4—4:坐標系與參數(shù)方程[來源:學科網(wǎng)ZXXK]
已知直線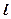 經(jīng)過點
經(jīng)過點 ,傾斜角
,傾斜角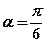 。
。
(1)寫出直線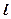 的參數(shù)方程;
的參數(shù)方程;
(2)設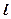 與曲線
與曲線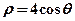 相交于兩點
相交于兩點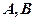 ,求點
,求點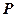 到
到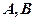 兩點的距離之積。
兩點的距離之積。
24.選修4—5:不等式證明選講
若不等式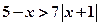 與不等式
與不等式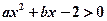 同解,而
同解,而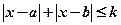 的解集為空集,求實數(shù)
的解集為空集,求實數(shù)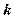 的取值范圍。
的取值范圍。
 選做題:請考生從22、23、24題中任選一題作答,并在答題卡上把所選題目的題號用2B鉛筆涂黑.注意所做題目的題號必須與所涂的題號一致,在答題卡選答區(qū)域指定位置答題.如果多做,則按所做的第一題計分.
選做題:請考生從22、23、24題中任選一題作答,并在答題卡上把所選題目的題號用2B鉛筆涂黑.注意所做題目的題號必須與所涂的題號一致,在答題卡選答區(qū)域指定位置答題.如果多做,則按所做的第一題計分. 選做題:請考生從22、23、24題中任選一題作答,并在答題卡上把所選題目的題號用2B鉛筆涂黑.注意所做題目的題號必須與所涂的題號一致,在答題卡選答區(qū)域指定位置答題.如果多做,則按所做的第一題計分.
選做題:請考生從22、23、24題中任選一題作答,并在答題卡上把所選題目的題號用2B鉛筆涂黑.注意所做題目的題號必須與所涂的題號一致,在答題卡選答區(qū)域指定位置答題.如果多做,則按所做的第一題計分.一、選擇題(每小題5分,共60分)
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
B
A
B
C
D
A
D
C
C
D
B
二、填空題(每小題5分,共20分)
13、(1,2); 14、20; 15、21;16、生高考模擬考試--數(shù)學理.files/image360.gif) .
.
三、解答題
17、解:(Ⅰ)當生高考模擬考試--數(shù)學理.files/image362.gif) 時,有
時,有生高考模擬考試--數(shù)學理.files/image364.gif) ,又
,又生高考模擬考試--數(shù)學理.files/image366.gif) ,所以
,所以生高考模擬考試--數(shù)學理.files/image368.gif) ……1分
……1分
當生高考模擬考試--數(shù)學理.files/image370.gif) 時,
時,生高考模擬考試--數(shù)學理.files/image372.gif)
=生高考模擬考試--數(shù)學理.files/image374.gif)
生高考模擬考試--數(shù)學理.files/image376.gif)
所以生高考模擬考試--數(shù)學理.files/image378.gif) ,且當
,且當生高考模擬考試--數(shù)學理.files/image362.gif) 時,
時,生高考模擬考試--數(shù)學理.files/image380.gif) ……3分
……3分
又生高考模擬考試--數(shù)學理.files/image382.gif) ,因此數(shù)列{
,因此數(shù)列{生高考模擬考試--數(shù)學理.files/image089.gif) }是以1為首項
}是以1為首項
且公差為2的等差數(shù)列,所以生高考模擬考試--數(shù)學理.files/image384.gif) ……2分
……2分
(Ⅱ)證明:(1)當生高考模擬考試--數(shù)學理.files/image362.gif) 時,
時,生高考模擬考試--數(shù)學理.files/image386.gif) ,
,生高考模擬考試--數(shù)學理.files/image388.gif) ,關系成立
……1分
,關系成立
……1分
(2)假設當生高考模擬考試--數(shù)學理.files/image390.gif) 時,關系成立,即
時,關系成立,即生高考模擬考試--數(shù)學理.files/image392.gif) ,則
,則生高考模擬考試--數(shù)學理.files/image394.gif)
……1分 那么生高考模擬考試--數(shù)學理.files/image396.gif)
生高考模擬考試--數(shù)學理.files/image398.gif) ,即當
,即當生高考模擬考試--數(shù)學理.files/image400.gif) 時關系也成立
時關系也成立
……3分 根據(jù)(1)和(2)知,關系式生高考模擬考試--數(shù)學理.files/image247.gif) 對任意
對任意生高考模擬考試--數(shù)學理.files/image237.gif) N*都成立 ……1分
N*都成立 ……1分
生高考模擬考試--數(shù)學理.files/image401.gif) 18、解:(Ⅰ)如圖,以C為原點,CA,CB,CC1所在直線分別為x軸,y軸,z軸建立空間直角坐標系,則
18、解:(Ⅰ)如圖,以C為原點,CA,CB,CC1所在直線分別為x軸,y軸,z軸建立空間直角坐標系,則生高考模擬考試--數(shù)學理.files/image403.gif) ,
,生高考模擬考試--數(shù)學理.files/image405.gif) ,
,生高考模擬考試--數(shù)學理.files/image407.gif) ,
,
生高考模擬考試--數(shù)學理.files/image409.gif) ,
,生高考模擬考試--數(shù)學理.files/image411.gif) ,
,生高考模擬考試--數(shù)學理.files/image413.gif) ……1分
……1分
設生高考模擬考試--數(shù)學理.files/image415.gif) ,則
,則生高考模擬考試--數(shù)學理.files/image417.gif) ,
,生高考模擬考試--數(shù)學理.files/image419.gif) ,
,
即AM⊥BC,又因為生高考模擬考試--數(shù)學理.files/image251.gif) ,且
,且生高考模擬考試--數(shù)學理.files/image421.gif) ,
,
所以 AM^平面生高考模擬考試--數(shù)學理.files/image253.gif) ……3分
……3分
(Ⅱ)生高考模擬考試--數(shù)學理.files/image423.gif) ,因為
,因為生高考模擬考試--數(shù)學理.files/image251.gif) ,所以
,所以生高考模擬考試--數(shù)學理.files/image425.gif) ,得
,得生高考模擬考試--數(shù)學理.files/image427.gif) ,
,
即生高考模擬考試--數(shù)學理.files/image429.gif) ,可得平面
,可得平面生高考模擬考試--數(shù)學理.files/image431.gif) 的一個法向量為
的一個法向量為生高考模擬考試--數(shù)學理.files/image433.gif) =
=生高考模擬考試--數(shù)學理.files/image435.gif) ……3分
……3分
生高考模擬考試--數(shù)學理.files/image437.gif) ,設平面
,設平面生高考模擬考試--數(shù)學理.files/image439.gif) 的一個法向量為
的一個法向量為生高考模擬考試--數(shù)學理.files/image441.gif) ,
,
則生高考模擬考試--數(shù)學理.files/image443.gif) 且
且生高考模擬考試--數(shù)學理.files/image445.gif) ,得
,得生高考模擬考試--數(shù)學理.files/image447.gif) ,
,生高考模擬考試--數(shù)學理.files/image449.gif) ,令
,令生高考模擬考試--數(shù)學理.files/image451.gif) ,得平面
,得平面生高考模擬考試--數(shù)學理.files/image439.gif) 的一個法向量為
的一個法向量為生高考模擬考試--數(shù)學理.files/image453.gif) =
=生高考模擬考試--數(shù)學理.files/image455.gif) ……3分設平面ABM與平面AB
……3分設平面ABM與平面AB生高考模擬考試--數(shù)學理.files/image335.gif) ,
,
則生高考模擬考試--數(shù)學理.files/image458.gif) ……2分
……2分
19、解:(Ⅰ)隨機變量甲、乙兩名運動員選擇的泳道相隔數(shù)X的分布列為:
X
0
1
2
3
4
5
6
生高考模擬考試--數(shù)學理.files/image067.gif)
生高考模擬考試--數(shù)學理.files/image461.gif)
生高考模擬考試--數(shù)學理.files/image463.gif)
生高考模擬考試--數(shù)學理.files/image465.gif)
生高考模擬考試--數(shù)學理.files/image467.gif)
生高考模擬考試--數(shù)學理.files/image469.gif)
生高考模擬考試--數(shù)學理.files/image471.gif)
生高考模擬考試--數(shù)學理.files/image473.gif)
……6分
泳道相隔數(shù)X的期望為:
E(X)=生高考模擬考試--數(shù)學理.files/image475.gif) ……2分
……2分
(Ⅱ)生高考模擬考試--數(shù)學理.files/image477.gif) ……4分
……4分
20、解:(Ⅰ)由生高考模擬考試--數(shù)學理.files/image479.gif) 得
得生高考模擬考試--數(shù)學理.files/image481.gif) ……2分
……2分
可得直線生高考模擬考試--數(shù)學理.files/image275.gif) 的方程為
的方程為生高考模擬考試--數(shù)學理.files/image484.gif) ,于是
,于是生高考模擬考試--數(shù)學理.files/image486.gif) ,
,
得生高考模擬考試--數(shù)學理.files/image488.gif) ,
,生高考模擬考試--數(shù)學理.files/image490.gif) ,
,生高考模擬考試--數(shù)學理.files/image492.gif) ,所以橢圓
,所以橢圓生高考模擬考試--數(shù)學理.files/image259.gif) 的方程為
的方程為生高考模擬考試--數(shù)學理.files/image494.gif) ……2分
……2分
(Ⅱ)設生高考模擬考試--數(shù)學理.files/image496.gif) ,由方程組
,由方程組生高考模擬考試--數(shù)學理.files/image498.gif) 得
得生高考模擬考試--數(shù)學理.files/image500.gif) ,
,
所以有生高考模擬考試--數(shù)學理.files/image502.gif) ,
,生高考模擬考試--數(shù)學理.files/image504.gif) ,且
,且生高考模擬考試--數(shù)學理.files/image506.gif) ,即
,即生高考模擬考試--數(shù)學理.files/image508.gif) ……2分
……2分
生高考模擬考試--數(shù)學理.files/image510.gif)
生高考模擬考試--數(shù)學理.files/image512.gif) ……2分
……2分
因為生高考模擬考試--數(shù)學理.files/image290.gif) ,所以
,所以生高考模擬考試--數(shù)學理.files/image514.gif) ,又
,又生高考模擬考試--數(shù)學理.files/image292.gif) ,所以
,所以生高考模擬考試--數(shù)學理.files/image286.gif) 是線段
是線段生高考模擬考試--數(shù)學理.files/image284.gif) 的中點,
的中點,
點生高考模擬考試--數(shù)學理.files/image286.gif) 的坐標為
的坐標為生高考模擬考試--數(shù)學理.files/image519.gif) ,即
,即生高考模擬考試--數(shù)學理.files/image286.gif) 的坐標是
的坐標是生高考模擬考試--數(shù)學理.files/image522.gif) ,因此
,因此
直線生高考模擬考試--數(shù)學理.files/image524.gif) 的方程為
的方程為生高考模擬考試--數(shù)學理.files/image526.gif) ,得點
,得點生高考模擬考試--數(shù)學理.files/image105.gif) 的坐標為(0,
的坐標為(0,生高考模擬考試--數(shù)學理.files/image529.gif) ),
),
所以生高考模擬考試--數(shù)學理.files/image531.gif) ……2分
……2分
因此生高考模擬考試--數(shù)學理.files/image533.gif)
所以當生高考模擬考試--數(shù)學理.files/image535.gif) ,即
,即生高考模擬考試--數(shù)學理.files/image537.gif) 時,
時,生高考模擬考試--數(shù)學理.files/image016.gif) 取得最大值,最大值為
取得最大值,最大值為生高考模擬考試--數(shù)學理.files/image540.gif) ……2分
……2分
21、解:(Ⅰ)生高考模擬考試--數(shù)學理.files/image542.gif)
生高考模擬考試--數(shù)學理.files/image544.gif)
生高考模擬考試--數(shù)學理.files/image546.gif) ……2分
……2分
若生高考模擬考試--數(shù)學理.files/image303.gif) ,則
,則生高考模擬考試--數(shù)學理.files/image549.gif) ,
,生高考模擬考試--數(shù)學理.files/image216.gif) 為R上的單調遞增函數(shù);
為R上的單調遞增函數(shù);
若生高考模擬考試--數(shù)學理.files/image552.gif) ,
,生高考模擬考試--數(shù)學理.files/image554.gif) 的解為
的解為生高考模擬考試--數(shù)學理.files/image556.gif) 或
或生高考模擬考試--數(shù)學理.files/image558.gif) ,
,生高考模擬考試--數(shù)學理.files/image560.gif) 的解為
的解為生高考模擬考試--數(shù)學理.files/image562.gif) ,
,
此時生高考模擬考試--數(shù)學理.files/image216.gif) 在區(qū)間
在區(qū)間生高考模擬考試--數(shù)學理.files/image564.gif) 單調遞增,在區(qū)間
單調遞增,在區(qū)間生高考模擬考試--數(shù)學理.files/image566.gif) 單調遞減;
單調遞減;
若生高考模擬考試--數(shù)學理.files/image568.gif) ,
,生高考模擬考試--數(shù)學理.files/image554.gif) 的解為
的解為生高考模擬考試--數(shù)學理.files/image570.gif) 或
或生高考模擬考試--數(shù)學理.files/image572.gif) ,
,生高考模擬考試--數(shù)學理.files/image560.gif) 的解為
的解為生高考模擬考試--數(shù)學理.files/image574.gif) ,
,
此時生高考模擬考試--數(shù)學理.files/image216.gif) 在區(qū)間
在區(qū)間生高考模擬考試--數(shù)學理.files/image576.gif) 單調遞增,在區(qū)間
單調遞增,在區(qū)間生高考模擬考試--數(shù)學理.files/image578.gif) 單調遞減……3分
單調遞減……3分
(Ⅱ)當生高考模擬考試--數(shù)學理.files/image303.gif) 時,
時,生高考模擬考試--數(shù)學理.files/image580.gif) ,
,生高考模擬考試--數(shù)學理.files/image582.gif) ,
,
因為生高考模擬考試--數(shù)學理.files/image584.gif) ,所以點
,所以點生高考模擬考試--數(shù)學理.files/image105.gif) (0,
(0,生高考模擬考試--數(shù)學理.files/image306.gif) )不在曲線
)不在曲線生高考模擬考試--數(shù)學理.files/image216.gif) 上,設過點
上,設過點生高考模擬考試--數(shù)學理.files/image105.gif) 的直線與曲線
的直線與曲線生高考模擬考試--數(shù)學理.files/image216.gif) 相切于點
相切于點生高考模擬考試--數(shù)學理.files/image588.gif) ,則切線方程為
,則切線方程為生高考模擬考試--數(shù)學理.files/image590.gif) ,所以有
,所以有生高考模擬考試--數(shù)學理.files/image592.gif) 及
及
生高考模擬考試--數(shù)學理.files/image594.gif) ,得
,得生高考模擬考試--數(shù)學理.files/image596.gif) ……2分 令
……2分 令生高考模擬考試--數(shù)學理.files/image598.gif) ,
,
則生高考模擬考試--數(shù)學理.files/image600.gif) ,
,
令生高考模擬考試--數(shù)學理.files/image602.gif) ,得
,得生高考模擬考試--數(shù)學理.files/image604.gif) ,
,生高考模擬考試--數(shù)學理.files/image606.gif) ,
,生高考模擬考試--數(shù)學理.files/image608.gif) ,可得
,可得生高考模擬考試--數(shù)學理.files/image610.gif) 在區(qū)間
在區(qū)間生高考模擬考試--數(shù)學理.files/image612.gif) 單調遞增,在區(qū)間
單調遞增,在區(qū)間生高考模擬考試--數(shù)學理.files/image614.gif) 單調遞減,所以
單調遞減,所以生高考模擬考試--數(shù)學理.files/image610.gif) 在
在生高考模擬考試--數(shù)學理.files/image616.gif) 時取極大值
時取極大值生高考模擬考試--數(shù)學理.files/image618.gif) ,
,
在生高考模擬考試--數(shù)學理.files/image620.gif) 時取極小值
時取極小值生高考模擬考試--數(shù)學理.files/image622.gif) ,在
,在生高考模擬考試--數(shù)學理.files/image624.gif) 時取極大值
時取極大值生高考模擬考試--數(shù)學理.files/image626.gif) ,又
,又生高考模擬考試--數(shù)學理.files/image628.gif) ,
,
生高考模擬考試--數(shù)學理.files/image630.gif) 所以
所以生高考模擬考試--數(shù)學理.files/image618.gif) 是
是生高考模擬考試--數(shù)學理.files/image610.gif) 的最大值
……3分
的最大值
……3分
如圖,過點生高考模擬考試--數(shù)學理.files/image105.gif) (0,
(0,生高考模擬考試--數(shù)學理.files/image306.gif) )有且只有一條直線與曲線
)有且只有一條直線與曲線生高考模擬考試--數(shù)學理.files/image216.gif)
相切等價于直線生高考模擬考試--數(shù)學理.files/image633.gif) 與曲線
與曲線生高考模擬考試--數(shù)學理.files/image598.gif)
有且只有一個交點,又當生高考模擬考試--數(shù)學理.files/image635.gif) 時,
時,生高考模擬考試--數(shù)學理.files/image637.gif) ,所以
,所以生高考模擬考試--數(shù)學理.files/image639.gif) 或
或生高考模擬考試--數(shù)學理.files/image641.gif) ……2分
……2分
生高考模擬考試--數(shù)學理.files/image642.gif) 22、(Ⅰ)證明:因為AB為⊙O直徑,
22、(Ⅰ)證明:因為AB為⊙O直徑,
所以 ∠ACB=90°,即 AC⊥BC,
因為D是弧生高考模擬考試--數(shù)學理.files/image313.gif) 的中點,由垂徑定理
的中點,由垂徑定理
得OD⊥BC,因此OD∥AC ……3分
又因為點O為AB的中點,所以點E為
BC的中點,所以OE=生高考模擬考試--數(shù)學理.files/image644.gif) AC ……2分
AC ……2分
(Ⅱ)證明:連結CD,因為PC是⊙O的切線,所以∠PCD=∠CAP,又∠P是公共角,所以 △PCD∽△PAC.得生高考模擬考試--數(shù)學理.files/image646.gif)
生高考模擬考試--數(shù)學理.files/image648.gif)
生高考模擬考試--數(shù)學理.files/image650.gif) ,得
,得生高考模擬考試--數(shù)學理.files/image652.gif) ……3分
……3分
因為D是弧生高考模擬考試--數(shù)學理.files/image313.gif) 的中點,所以
的中點,所以生高考模擬考試--數(shù)學理.files/image654.gif) ,因此
,因此生高考模擬考試--數(shù)學理.files/image326.gif) ……2分
……2分
23、解:(Ⅰ)曲線生高考模擬考試--數(shù)學理.files/image331.gif) 上的動點
上的動點生高考模擬考試--數(shù)學理.files/image259.gif) 的坐標為(
的坐標為(生高考模擬考試--數(shù)學理.files/image656.gif) ,
,生高考模擬考試--數(shù)學理.files/image658.gif) ),坐標原點
),坐標原點生高考模擬考試--數(shù)學理.files/image273.gif) (0,0),
(0,0),
設P的坐標為(生高考模擬考試--數(shù)學理.files/image135.gif) ,
,生高考模擬考試--數(shù)學理.files/image137.gif) ),則由中點坐標公式得
),則由中點坐標公式得生高考模擬考試--數(shù)學理.files/image663.gif) ,
,生高考模擬考試--數(shù)學理.files/image665.gif) ,所以點P 的坐標為(
,所以點P 的坐標為(生高考模擬考試--數(shù)學理.files/image667.gif) ,
,生高考模擬考試--數(shù)學理.files/image669.gif) )……3分
)……3分
因此點生高考模擬考試--數(shù)學理.files/image105.gif) 的軌跡的參數(shù)方程為
的軌跡的參數(shù)方程為生高考模擬考試--數(shù)學理.files/image671.gif) (
(生高考模擬考試--數(shù)學理.files/image335.gif) 為參數(shù),且
為參數(shù),且生高考模擬考試--數(shù)學理.files/image337.gif) ),
),
消去參數(shù)生高考模擬考試--數(shù)學理.files/image335.gif) 得點
得點生高考模擬考試--數(shù)學理.files/image105.gif) 軌跡的直角坐標方程為
軌跡的直角坐標方程為生高考模擬考試--數(shù)學理.files/image674.gif) ……2分
……2分
(Ⅱ)由直角坐標與極坐標關系生高考模擬考試--數(shù)學理.files/image676.gif) 得直線
得直線生高考模擬考試--數(shù)學理.files/image230.gif) 的直角坐標方程為
的直角坐標方程為
生高考模擬考試--數(shù)學理.files/image678.gif) ……2分 又由(Ⅰ)知點
……2分 又由(Ⅰ)知點生高考模擬考試--數(shù)學理.files/image105.gif) 的軌跡為圓心在原點半徑為2的圓,
的軌跡為圓心在原點半徑為2的圓,
因為原點(0,0)到直線生高考模擬考試--數(shù)學理.files/image678.gif) 的距離為
的距離為生高考模擬考試--數(shù)學理.files/image680.gif)
所以點生高考模擬考試--數(shù)學理.files/image105.gif) 到直線
到直線生高考模擬考試--數(shù)學理.files/image230.gif) 距離的最大值
距離的最大值生高考模擬考試--數(shù)學理.files/image682.gif) ……3分
……3分
24、解:(Ⅰ)由題意得生高考模擬考試--數(shù)學理.files/image684.gif) ,即
,即生高考模擬考試--數(shù)學理.files/image686.gif) 得
得生高考模擬考試--數(shù)學理.files/image688.gif) ……2分
……2分
因為生高考模擬考試--數(shù)學理.files/image690.gif)
所以生高考模擬考試--數(shù)學理.files/image135.gif) 的取值范圍是[0,6] ……3分
的取值范圍是[0,6] ……3分
(Ⅱ)生高考模擬考試--數(shù)學理.files/image692.gif) ,
,
因為對于生高考模擬考試--數(shù)學理.files/image694.gif) ,由絕對值的三角不等式得
,由絕對值的三角不等式得
生高考模擬考試--數(shù)學理.files/image696.gif)
生高考模擬考試--數(shù)學理.files/image698.gif) ……3分
……3分
于是有生高考模擬考試--數(shù)學理.files/image700.gif) ,得
,得生高考模擬考試--數(shù)學理.files/image702.gif) ,即
,即生高考模擬考試--數(shù)學理.files/image050.gif) 的取值范圍是
的取值范圍是生高考模擬考試--數(shù)學理.files/image704.gif) ……2分
……2分
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com