
題目列表(包括答案和解析)
(本題12分)已知橢圓![]() 的離心率
的離心率![]() ,短軸長為
,短軸長為![]() 。
。
(1)求橢圓的標準方程;
(2)若直線![]() :
:![]() 交橢圓于
交橢圓于![]() 兩點,向量
兩點,向量![]() ,滿足
,滿足![]() .證明:
.證明:![]() 的面積為定值。 (
的面積為定值。 (![]() 為坐標原點)
為坐標原點)
(本題12分)
已知橢圓 的右焦點為F,上頂點為A,P為C
的右焦點為F,上頂點為A,P為C 上任一點,MN是圓
上任一點,MN是圓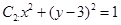 的一條直徑,若與AF平行且在y軸上的截距為
的一條直徑,若與AF平行且在y軸上的截距為 的直線
的直線 恰好與圓
恰好與圓 相切.
相切.
(Ⅰ)求橢圓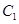 的離心率;
的離心率;
(Ⅱ)若 的最大值為49,求橢圓C
的最大值為49,求橢圓C 的方程.
的方程.
(本題12分)
已知橢圓 的右焦點為F,上頂點為A,P為C
的右焦點為F,上頂點為A,P為C 上任一點,MN是圓
上任一點,MN是圓 的一條直徑,若與AF平行且在y軸上的截距為
的一條直徑,若與AF平行且在y軸上的截距為 的直線
的直線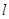 恰好與圓
恰好與圓 相切.
相切.
(Ⅰ)求橢圓 的離心率;
的離心率;
(Ⅱ)若 的最大值為49,求橢圓C
的最大值為49,求橢圓C 的方程.
的方程.
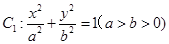 的右焦點為F,上頂點為A,P為C
的右焦點為F,上頂點為A,P為C 上任一點,MN是圓
上任一點,MN是圓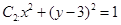 的一條直徑,若與AF平行且在y軸上的截距為
的一條直徑,若與AF平行且在y軸上的截距為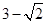 的直線
的直線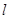 恰好與圓
恰好與圓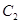 相切.
相切.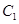 的離心率;
的離心率;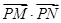 的最大值為49,求橢圓C
的最大值為49,求橢圓C 的方程.
的方程.(本題滿分12分)已知橢圓 的離心率為
的離心率為 ,
,
直線 與以原點為圓心、以橢圓
與以原點為圓心、以橢圓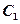 的短半軸長為半徑的圓相切.
的短半軸長為半徑的圓相切.
(Ⅰ)求橢圓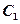 的方程;
的方程;
(Ⅱ)設(shè)橢圓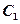 的左焦點為F1,右焦點為F2,直線
的左焦點為F1,右焦點為F2,直線 過點F1,且垂直于橢圓的長軸,動直線
過點F1,且垂直于橢圓的長軸,動直線 垂直
垂直 于點P,線段PF2的垂直平分線交
于點P,線段PF2的垂直平分線交 于點M,求點M的軌跡C2的方程;
于點M,求點M的軌跡C2的方程;
(Ⅲ)若AC、BD為橢圓C1的兩條相互垂直的弦,垂足為右焦點F2,求四邊形ABCD的面積的最小值.
一、選擇題:本大題共12小題,每小題5分,共60分。
題號
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
B
A
C
B
C
B
C
C
A
A
D
二、填空題:本大題共4小題,每小題4分,共16分
13、 -1 14、 24/5 15、 16/3 16、 ① ②
解:由學(xué)單元練習(xí)-人教大綱本.files/image151.gif) 得 P ( 1,-1)
得 P ( 1,-1)
據(jù)題意,直線l與直線學(xué)單元練習(xí)-人教大綱本.files/image153.gif) 垂直,故l斜率
垂直,故l斜率學(xué)單元練習(xí)-人教大綱本.files/image155.gif)
∴ 直線l方程為 學(xué)單元練習(xí)-人教大綱本.files/image157.gif) 即
即 學(xué)單元練習(xí)-人教大綱本.files/image159.gif) .
.
解:連結(jié)PO,得學(xué)單元練習(xí)-人教大綱本.files/image161.gif)
學(xué)單元練習(xí)-人教大綱本.files/image163.gif) 當PO通過圓心時有最大值和最小值
當PO通過圓心時有最大值和最小值學(xué)單元練習(xí)-人教大綱本.files/image165.gif)
學(xué)單元練習(xí)-人教大綱本.files/image167.gif)
學(xué)單元練習(xí)-人教大綱本.files/image169.gif)
學(xué)單元練習(xí)-人教大綱本.files/image171.gif)
解:設(shè)生產(chǎn)甲、乙兩種肥料各學(xué)單元練習(xí)-人教大綱本.files/image173.gif) 車皮,利潤總額為
車皮,利潤總額為學(xué)單元練習(xí)-人教大綱本.files/image175.gif) 元,那么
元,那么
學(xué)單元練習(xí)-人教大綱本.files/image177.gif)
學(xué)單元練習(xí)-人教大綱本.files/image179.gif)
畫圖得當學(xué)單元練習(xí)-人教大綱本.files/image181.gif) 時總額
時總額學(xué)單元練習(xí)-人教大綱本.files/image175.gif) 的最大值為30000
的最大值為30000
解:(1)學(xué)單元練習(xí)-人教大綱本.files/image183.gif)
(2)學(xué)單元練習(xí)-人教大綱本.files/image185.gif) 或0
或0
解:(1)設(shè)A(x1,y1),B(x2,y2),AB的方程為y-1=k(x-2) 即y=kx+1-2k①
∵離心率e=學(xué)單元練習(xí)-人教大綱本.files/image187.gif) ∴橢圓方程可化為
∴橢圓方程可化為學(xué)單元練習(xí)-人教大綱本.files/image189.gif) ②
②
將①代入②得(1+2k2)x2+4(1-2k)?kx+2(1-2k)2-2b2=0
∵x1+x2=學(xué)單元練習(xí)-人教大綱本.files/image191.gif) ∴k=-1
∴k=-1
∴x1x2=學(xué)單元練習(xí)-人教大綱本.files/image193.gif) 又
又學(xué)單元練習(xí)-人教大綱本.files/image195.gif) ∴
∴學(xué)單元練習(xí)-人教大綱本.files/image197.gif)
即學(xué)單元練習(xí)-人教大綱本.files/image199.gif) ∴b2=8 ∴
∴b2=8 ∴學(xué)單元練習(xí)-人教大綱本.files/image201.gif)
(2)設(shè)學(xué)單元練習(xí)-人教大綱本.files/image203.gif) (不妨設(shè)m<n)則由第二定義知
(不妨設(shè)m<n)則由第二定義知學(xué)單元練習(xí)-人教大綱本.files/image205.gif)
即學(xué)單元練習(xí)-人教大綱本.files/image207.gif) 或
或學(xué)單元練習(xí)-人教大綱本.files/image209.gif)
∴學(xué)單元練習(xí)-人教大綱本.files/image211.gif) 或
或學(xué)單元練習(xí)-人教大綱本.files/image213.gif)
解:由已知得 A (-1, 0 )、B ( 1, 0 ),
設(shè) P ( x, y ), C ( x0, y0 ) , 則 D (x0, -y0 ),
由A、C、P三點共線得 學(xué)單元練習(xí)-人教大綱本.files/image215.gif) ①
①
由D、B、P三點共線得 學(xué)單元練習(xí)-人教大綱本.files/image217.gif) ②
②
①×② 得 學(xué)單元練習(xí)-人教大綱本.files/image219.gif) ③
③
又 x02 + y02 = 1, ∴ y02 = 1-x02 代入③得 x2-y2 = 1,
即點P在雙曲線x2-y2 = 1上, 故由雙曲線定義知,存在兩個定點E (-學(xué)單元練習(xí)-人教大綱本.files/image105.gif) , 0 )、
, 0 )、
F (學(xué)單元練習(xí)-人教大綱本.files/image105.gif) , 0 )(即此雙曲線的焦點),使 | | PE |-| PF | | = 2 (即此雙曲線的實軸長) 為定值.
, 0 )(即此雙曲線的焦點),使 | | PE |-| PF | | = 2 (即此雙曲線的實軸長) 為定值.
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com