
【題目】設y=kx,是否存在實數k,使得代數式(x2﹣y2)(4x2﹣y2)+3x2(4x2﹣y2)能化簡為x4?若能,請求出所有滿足條件的k的值;若不能,請說明理由.
【答案】解:能; (x2﹣y2)(4x2﹣y2)+3x2(4x2﹣y2)
=(4x2﹣y2)(x2﹣y2+3x2)
=(4x2﹣y2)2 ,
當y=kx,原式=(4x2﹣k2x2)2=(4﹣k2)2x4 ,
令(4﹣k2)2=1,解得k=± ![]() 或±
或± ![]() ,
,
即當k=± ![]() 或±
或± ![]() 時,原代數式可化簡為x4
時,原代數式可化簡為x4
【解析】先利用因式分解得到原式=(4x2﹣y2)(x2﹣y2+3x2)=(4x2﹣y2)2 , 再把當y=kx代入得到原式=(4x2﹣k2x2)2=(4﹣k2)x4 , 所以當4﹣k2=1滿足條件,然后解關于k的方程即可.
【考點精析】根據題目的已知條件,利用因式分解的應用的相關知識可以得到問題的答案,需要掌握因式分解是整式乘法的逆向變形,可以應用與數字計算、求值、整除性問題、判斷三角形的形狀、解方程.


 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,AB=4cm,∠ADC=120°,點E,F同時由A,C兩點出發,分別沿AB,CB方向向點B勻速移動(到點B為止),點E的速度為1cm/s,點F的速度為2cm/s,經過t秒△DEF為等邊三角形,則t的值為( ) 
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,自左至右,第1個圖由1個正六邊形、6個正方形和6個等邊三角形組成;第2個圖由2個正六邊形、11個正方形和10個等邊三角形組成;第3個圖由3個正六邊形、16個正方形和14個等邊三角形組成;…按照此規律,第![]() 個圖中正方形和等邊三角形的個數之和為 個.
個圖中正方形和等邊三角形的個數之和為 個.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知AD∥BC,AB⊥AD,點E,點F分別在射線AD,射線BC上.若點E與點B關于AC對稱,點E與點F關于BD對稱,AC與BD相交于點G,則( ) 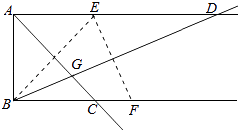
A.1+tan∠ADB= ![]()
B.2BC=5CF
C.∠AEB+22°=∠DEF
D.4cos∠AGB= ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個布袋中裝有只有顏色不同的a(a>12)個球,分別是2個白球,4個黑球,6個紅球和b個黃球,從中任意摸出一個球,把摸出白球,黑球,紅球的概率繪制成統計圖(未繪制完整).請補全該統計圖并求出 ![]() 的值.
的值. 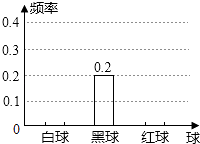
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是半圓O的直徑,點C在半圓O上,AB=5cm,AC=4cm.D是弧BC上的一個動點(含端點B,不含端點C),連接AD,過點C作CE⊥AD于E,連接BE,在點D移動的過程中,BE的取值范圍是 . 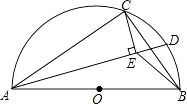
查看答案和解析>>
科目:初中數學 來源: 題型:
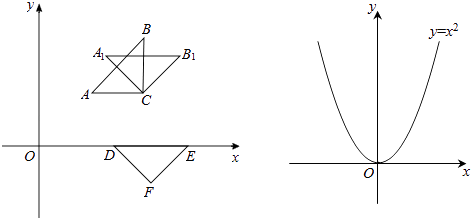
【題目】小明合作學習小組在探究旋轉、平移變換.如圖△ABC,DEF均為等腰直角三角形,各頂點坐標分別為A(1,1),B(2,2),C(2,1),D( ![]() ,0),E(2
,0),E(2 ![]() ,0),F(
,0),F( ![]() ,﹣
,﹣ ![]() ).
).
(1)他們將△ABC繞C點按順時針方向旋轉45°得到△A1B1C1 . 請你寫出點A1 , B1的坐標,并判斷A1C和DF的位置關系;
(2)他們將△ABC繞原點按順時針方向旋轉45°,發現旋轉后的三角形恰好有兩個頂點落在拋物線y=2 ![]() x2+bx+c上,請你求出符合條件的拋物線解析式;
x2+bx+c上,請你求出符合條件的拋物線解析式;
(3)他們繼續探究,發現將△ABC繞某個點旋轉45°,若旋轉后的三角形恰好有兩個頂點落在拋物線y=x2上,則可求出旋轉后三角形的直角頂點P的坐標,請你直接寫出點P的所有坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
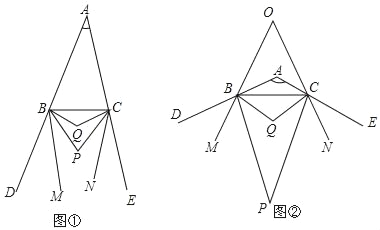
【題目】已知:如圖①,BP、CP分別平分△ABC的外角∠CBD、∠BCE,BQ、CQ分別平分∠PBC、∠PCB,BM、CN分別是∠PBD、∠PCE的角平分線.
(1)當∠BAC=40°時,∠BPC= ,∠BQC= ;
(2)當BM∥CN時,求∠BAC的度數;
(3)如圖②,當∠BAC=120°時,BM、CN所在直線交于點O,直接寫出∠BOC的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com