
【題目】已知拋物線![]() 的解析式為
的解析式為![]() ,(與
,(與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() (點(diǎn)
(點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 左側(cè)),與
左側(cè)),與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,項(xiàng)點(diǎn)為
,項(xiàng)點(diǎn)為![]() .
.
(1)求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(2)若將拋物線![]() 沿著直線
沿著直線![]() 的方向平移得到拋物線
的方向平移得到拋物線![]() ;
;
①當(dāng)拋物線![]() 與直線
與直線![]() 只有一個(gè)公共點(diǎn)時(shí),求拋物線
只有一個(gè)公共點(diǎn)時(shí),求拋物線![]() 的解析式;
的解析式;
②點(diǎn)![]() 是①中拋物線上一點(diǎn),若
是①中拋物線上一點(diǎn),若![]() 且
且![]() 為整數(shù),求滿足條件的點(diǎn)
為整數(shù),求滿足條件的點(diǎn)![]() 的個(gè)數(shù).
的個(gè)數(shù).
【答案】(1)點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() ;(2)①
;(2)①![]() ,②滿足條件的
,②滿足條件的![]() 點(diǎn)有
點(diǎn)有![]() 個(gè).
個(gè).
【解析】
(1)令y=0求出x,可得點(diǎn)A、B的坐標(biāo);令x=0求出y,可得點(diǎn)D的坐標(biāo);將二次函數(shù)的解析式化為頂點(diǎn)式即可得點(diǎn)P的坐標(biāo);
(2)①先求出直線PD的解析式,由拋物線![]() 的頂點(diǎn)在直線PD上移動(dòng)可設(shè)出拋物線
的頂點(diǎn)在直線PD上移動(dòng)可設(shè)出拋物線![]() 的頂點(diǎn)式,根據(jù)拋物線
的頂點(diǎn)式,根據(jù)拋物線![]() 與直線
與直線![]() 只有一個(gè)公共點(diǎn),利用
只有一個(gè)公共點(diǎn),利用![]() 可求得拋物線的頂點(diǎn)坐標(biāo),即可求得其解析式;
可求得拋物線的頂點(diǎn)坐標(biāo),即可求得其解析式;
②先求出當(dāng)![]() 、
、![]() 時(shí)
時(shí)![]() 的取值,根據(jù)二次函數(shù)的頂點(diǎn)式及其圖象性質(zhì)可分別求得當(dāng)
的取值,根據(jù)二次函數(shù)的頂點(diǎn)式及其圖象性質(zhì)可分別求得當(dāng)![]() 、
、![]() 時(shí)
時(shí)![]() 的取值范圍,進(jìn)而得出
的取值范圍,進(jìn)而得出![]() 的整數(shù)值,即可求出滿足條件的點(diǎn)
的整數(shù)值,即可求出滿足條件的點(diǎn)![]() 的個(gè)數(shù).
的個(gè)數(shù).
解:(1)取![]() ,即
,即![]()
解得:![]()
則點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]()
取![]() ,得
,得![]()
則點(diǎn)![]()
又![]()
則點(diǎn)![]()
(2)①設(shè)直線![]() 的解析式為
的解析式為![]()
![]() 點(diǎn)
點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]()
![]()
解得![]()
![]() 直線
直線![]() 的解析式為
的解析式為![]() ,
,
![]() 拋物線
拋物線![]() 沿著直線
沿著直線 ![]() 的方向平移得到拋物線
的方向平移得到拋物線![]()
![]() 平移后
平移后![]() 的頂點(diǎn)坐標(biāo)為
的頂點(diǎn)坐標(biāo)為![]()
設(shè)平移后![]() 解析式為
解析式為![]()
又拋物線![]() 與直線
與直線![]() 只有一個(gè)公共點(diǎn)
只有一個(gè)公共點(diǎn)
令![]()
整理得:![]()
則![]() ,即
,即![]()
解得![]()
![]() 平移后所得拋物線
平移后所得拋物線![]() 的解析式為
的解析式為![]()
即![]()
②![]() 的頂點(diǎn)為
的頂點(diǎn)為![]()
∵當(dāng)![]() 時(shí),
時(shí),![]() 時(shí)
時(shí)![]()
∴當(dāng)![]() 時(shí),
時(shí),![]()
則![]() 有
有![]() 個(gè)整數(shù)
個(gè)整數(shù)
當(dāng)![]() 時(shí),
時(shí),![]()
則![]() 有
有![]() 個(gè)整數(shù)
個(gè)整數(shù)
拋物線是連續(xù)的,所以![]() 可以取到當(dāng)
可以取到當(dāng)![]() 時(shí)的函數(shù)值的所有整數(shù),
時(shí)的函數(shù)值的所有整數(shù),
故滿足條件的![]() 點(diǎn)有
點(diǎn)有![]() 個(gè).
個(gè).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
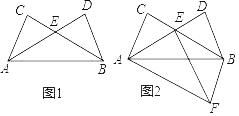
【題目】如圖1,點(diǎn)C、D是線段AB同側(cè)兩點(diǎn),且AC=BD,∠CAB=∠DBA,連接BC,AD交于點(diǎn) E.
(1)求證:AE=BE;
(2)如圖2,△ABF與△ABD關(guān)于直線AB對(duì)稱,連接EF.
①判斷四邊形ACBF的形狀,并說(shuō)明理由;
②若∠DAB=30°,AE=5,DE=3,求線段EF的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】長(zhǎng)城公司為希望小學(xué)捐贈(zèng)甲、乙兩種品牌的體育器材,甲品牌有A、B、C三種型號(hào),乙品牌有D、E兩種型號(hào),現(xiàn)要從甲、乙兩種品牌的器材中各選購(gòu)一種型號(hào)進(jìn)行捐贈(zèng).
(1)下列事件是不可能事件的是
A.選購(gòu)甲品牌的B型號(hào);
B.選購(gòu)甲品牌的C型號(hào)和乙品牌的D型號(hào);
C.既選購(gòu)甲品牌也選購(gòu)乙品牌;
D.只選購(gòu)乙品牌的E型號(hào).
(2)用列表法或樹狀圖法,寫出所有的選購(gòu)方案,若每種方案被選中的可能性相同,求A型號(hào)的器材被選中的概率?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
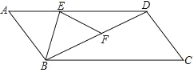
【題目】.E為□ABCD邊AD上一點(diǎn),將ABE沿BE翻折得到FBE,點(diǎn)F在BD上,且EF=DF.若∠C=52°,則∠ABE=____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
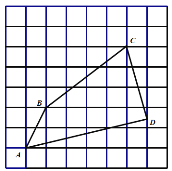
【題目】如圖,在每個(gè)小正方形的邊長(zhǎng)為的網(wǎng)格中,點(diǎn)![]() 均在格點(diǎn)上,
均在格點(diǎn)上,![]() 為小正方形邊中點(diǎn).
為小正方形邊中點(diǎn).
(1)![]() 的長(zhǎng)等于 ______;
的長(zhǎng)等于 ______;
(2)請(qǐng)?jiān)谌鐖D所示的網(wǎng)格中,用無(wú)刻度的直尺,畫出一個(gè)點(diǎn)![]() ,使其滿足
,使其滿足![]() 說(shuō)明點(diǎn)
說(shuō)明點(diǎn)![]() 的位置是如何找到的(不要求證明)______.
的位置是如何找到的(不要求證明)______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,![]() 是
是![]() 的外接圓,
的外接圓,![]() 為直徑,
為直徑,![]() 的平分線交O于點(diǎn)D,過(guò)點(diǎn)D作
的平分線交O于點(diǎn)D,過(guò)點(diǎn)D作![]() ,分別交
,分別交![]() ,
,![]() 的延長(zhǎng)線于點(diǎn)E,F.
的延長(zhǎng)線于點(diǎn)E,F.
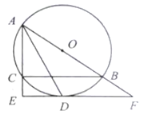
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)填空:
①當(dāng)![]() 的度數(shù)為_________時(shí),四邊形
的度數(shù)為_________時(shí),四邊形![]() 為菱形;
為菱形;
②若![]() 的半徑為
的半徑為![]() ,
,![]() ,則
,則![]() 的長(zhǎng)為_________.
的長(zhǎng)為_________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示的曲邊三角形可按下述方法作出:作等邊三角形![]() ;分別以點(diǎn)
;分別以點(diǎn)![]() ,
,![]() ,
,![]() 為圓心,以
為圓心,以![]() 的長(zhǎng)為半徑作
的長(zhǎng)為半徑作![]() ,
,![]() ,
,![]() .三段弧所圍成的圖形就是一個(gè)曲邊三角形,如果一個(gè)曲邊三角形的周長(zhǎng)為
.三段弧所圍成的圖形就是一個(gè)曲邊三角形,如果一個(gè)曲邊三角形的周長(zhǎng)為![]() ,那么這個(gè)曲邊三角形的面積是___________.
,那么這個(gè)曲邊三角形的面積是___________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知拋物線與x軸交于A(﹣1,0)、E(3,0)兩點(diǎn),與y軸交于點(diǎn)B(0,3).
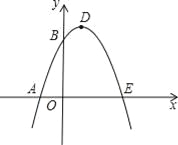
(1)求拋物線的解析式;
(2)設(shè)拋物線頂點(diǎn)為D,求四邊形AEDB的面積;
(3)△AOB與△DBE是否相似?如果相似,請(qǐng)給以證明;如果不相似,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】小張用4張相同的小紙條做成甲、乙、丙、丁4支簽,放在一個(gè)盒子中,攪勻后先從盒子中任意抽出1支簽(不放回),再?gòu)氖S嗟?/span>3支簽中任意抽出1支簽.
(1)小張第一次抽到的是乙簽的概率是 ;
(2)求抽出的兩支簽中,1支為甲簽、1支為丙簽的概率(用畫樹狀圖或列表法求解).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com