
【題目】如圖,等腰△ABC中,AB=AC,BD,CE分別是邊AC,AB上的中線,BD與CE相交于點O,點M,N分別為線段BO和CO的中點.求證:四邊形EDNM是矩形.

【答案】見解析
【解析】試題分析:由題意得出ED是△ABC的中位線,得出ED∥BC,ED=![]() BC,由題意得出MN是△OBC的中位線,得出MN∥BC,MN=
BC,由題意得出MN是△OBC的中位線,得出MN∥BC,MN=![]() BC,因此ED∥MN,ED=MN,證明四邊形EDNM是平行四邊形,再由SAS證明△ABD≌△ACE,得出BD=CE,證出DM=EN,即可得出四邊形EDNM是矩形.
BC,因此ED∥MN,ED=MN,證明四邊形EDNM是平行四邊形,再由SAS證明△ABD≌△ACE,得出BD=CE,證出DM=EN,即可得出四邊形EDNM是矩形.
試題解析:證明:∵BD,CE分別是AC,AB邊上的中線
∴AE=![]() AB,AD=
AB,AD=![]() AC,ED是△ABC的中位線
AC,ED是△ABC的中位線
∴ED∥BC,ED=![]() BC.
BC.
∵點M,N分別為線段BO和CO的中點
∴OM=BM,ON=CN,MN是△OBC的中位線
∴MN∥BC,MN=![]() BC
BC
∴ED∥MN,ED=MN
∴四邊形EDNM是平行四邊形
∴OE=ON,OD=OM.∵AB=AC
∴AE=AD.
在△ABD和△ACE中,
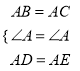
∴△ABD≌△ACE
∴BD=CE
∴EO+ON+CN=BM+OM+OD
∴3OE=3OM,
即OE=OM.
又∵DM=2OM,EN=2OE,
∴DM=EN
∴四邊形EDNM是矩形


 陽光課堂課時作業系列答案
陽光課堂課時作業系列答案科目:初中數學 來源: 題型:
【題目】如果∠α和∠β互補,且∠α<∠β,下列表達式:①90°﹣∠α;②∠β﹣90°;③![]() (∠β+∠α);④
(∠β+∠α);④![]() (∠β﹣∠α)中,等于∠α的余角的式子有( )
(∠β﹣∠α)中,等于∠α的余角的式子有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,點D,E分別在AB,AC上,CE=BC,連接CD,將線段CD繞點C按順時針方向旋轉90°后得CF,連接EF.
(1)補充完成圖形;
(2)若EF∥CD,求證:∠BDC=90°.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明家的洗手盆上裝有一種抬啟式水龍頭(如圖1),完全開啟后,水流路線呈拋物線,把手端點A,出水口B和落水點C恰好在同一直線上,點A至出水管BD的距離為12cm,洗手盆及水龍頭的相關數據如圖2所示,現用高10.2cm的圓柱型水杯去接水,若水流所在拋物線經過點D和杯子上底面中心E,則點E到洗手盆內側的距離EH為cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在一條東西向的雙軌鐵路上迎面駛來一快一慢兩列火車,快車長![]() (單位長度)。慢車長
(單位長度)。慢車長![]() (單位長度),設正在行駛途中的某一時刻,如圖,以兩車之間的某點
(單位長度),設正在行駛途中的某一時刻,如圖,以兩車之間的某點![]() 為原點,取向右方向為正方向畫數軸,此時快車
為原點,取向右方向為正方向畫數軸,此時快車![]() 在數軸上表示的數是
在數軸上表示的數是![]() ,慢車頭
,慢車頭![]() 在數軸上表示的數是
在數軸上表示的數是![]() ,若快車
,若快車![]() 以
以![]() 個單位長度/秒的速度向右勻速繼續行駛,同時慢車
個單位長度/秒的速度向右勻速繼續行駛,同時慢車![]() 以
以![]() 個單位長度/秒的速度向左勻速繼續行駛,且
個單位長度/秒的速度向左勻速繼續行駛,且![]() 與
與![]() 互為相反數.
互為相反數.
(1)求此時刻快車頭![]() 與慢車頭
與慢車頭![]() 之間相距多少單位長度?
之間相距多少單位長度?
(2)從此時刻開始算起,問再行駛多少秒兩列火車行駛到車頭![]() 、
、![]() 相距
相距![]() 個單位長度?
個單位長度?
(3)此時在快車![]() 上有一位愛到腦筋的七年級學生乘客
上有一位愛到腦筋的七年級學生乘客![]() ,他發現行駛中有一段時間,他的位置
,他發現行駛中有一段時間,他的位置![]() 到兩列火車頭
到兩列火車頭![]() 、
、![]() 的距離和加上到兩列火車尾
的距離和加上到兩列火車尾![]() 、
、![]() 的距離和是一個不變的值(即
的距離和是一個不變的值(即![]() 為定值),你認為學生
為定值),你認為學生![]() 發現的這一結論是否正確?若正確,求出增定值及所持續的時間;若不正確,請說明理由.
發現的這一結論是否正確?若正確,求出增定值及所持續的時間;若不正確,請說明理由.
![]()
附加題:
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】做大小兩個長方體紙盒,尺寸如圖(單位:cm)
(1)用a、b、c的代數式表示做這兩個紙盒共需用料多少cm2.
(2)試計算做大紙盒比做小紙盒多用料多少cm2.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com