
【題目】觀察下列兩個等式:![]() ,
,![]() ,給出定義如下:我們稱使等式a﹣b=ab+1的成立的一對有理數a,b為“共生有理數對”,記為(a,b),如:數對
,給出定義如下:我們稱使等式a﹣b=ab+1的成立的一對有理數a,b為“共生有理數對”,記為(a,b),如:數對![]() ,
,![]() ,都是“共生有理數對”.
,都是“共生有理數對”.
(1)數對![]() ,
,![]() 中是“共生有理數對”的是 ;
中是“共生有理數對”的是 ;
(2)若(m,n)是“共生有理數對”,則(﹣n,﹣m) “共生有理數對”(填“是”或“不是”);
(3)請再寫出一對符合條件的“共生有理數對”為 ;(注意:不能與題目中已有的“共生有理數對”重復)
(4)若(a,3)是“共生有理數對”,求a的值.
【答案】(1)![]() ;(2)是;(3)
;(2)是;(3)![]() 或
或![]() 等;(4)a=-2
等;(4)a=-2
【解析】
(1)根據“共生有理數對”的定義即可判斷;
(2)根據“共生有理數對”的定義即可解決問題;
(3)根據“共生有理數對”的定義即可判斷;
(4)根據“共生有理數對”的定義,構建方程即可解決問題.
解:(1)-2-1=-3,-2×1+1=1,
∴-2-1≠-2×1+1,
∴(-2,1)不是“共生有理數對”,
∵3-![]() =
=![]() ,3×
,3×![]() +1=
+1=![]() ,
,
∴3-![]() =3×
=3×![]() +1,
+1,
∴(3,![]() )是“共生有理數對”;
)是“共生有理數對”;
(2)是.
理由:- n -(- m)=- n + m =m-n,
-n(-m)+1=mn+1,
∵(m,n)是“共生有理數對”,
∴m-n=mn+1,
∴-n+m=mn+1,
∴(-n,-m)是“共生有理數對”;
(3)![]() 或
或![]() 等;
等;
理由:∵![]() ,
,![]() ,
,
∴![]()
∴![]() 是“共生有理數對”,
是“共生有理數對”,
∵![]() ,
,![]() ,
,
∴![]()
∴![]() 是“共生有理數對”;
是“共生有理數對”;
(4)由題意得:
a-3=3a+1,
解得a=-2.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】某電視臺的一檔娛樂性節目中,在游戲PK環節,為了隨機分選游戲雙方的組員,主持人設計了以下游戲:用不透明的白布包住三根顏色長短相同的細繩AA1、BB1、CC1,只露出它們的頭和尾(如圖所示),由甲、乙兩位嘉賓分別從白布兩端各選一根細繩,并拉出,若兩人選中同一根細繩,則兩人同隊,否則互為反方隊員.
(1)若甲嘉賓從中任意選擇一根細繩拉出,求他恰好抽出細繩AA1的概率;
(2)請用畫樹狀圖法或列表法,求甲、乙兩位嘉賓能分為同隊的概率.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
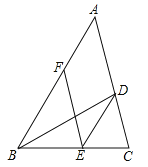
【題目】如圖,BD是△ABC的角平分線,點E,F分別在BC,AB上,且DE∥AB,BE=AF.
(1)求證:四邊形ADEF是平行四邊形;
(2)若∠ABC=60°,BD=4,求平行四邊形ADEF的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在數軸上,點A表示1,現將點A沿數軸做如下移動,第一次點A向左移動3個單位長度到達點A1,第二次將點A1向右移動6個單位長度到達點A2,第三次將點A2向左移動9個單位長度到達點A3,按照這種規律下去,第n次移動到點An,如果點An,與原點的距離不少于20,那么n的最小值是( )

A. 11B. 12C. 13D. 20
查看答案和解析>>
科目:初中數學 來源: 題型:
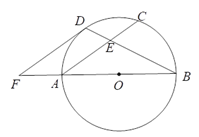
【題目】如圖,AB是⊙O的直徑,C是⊙O上一點,D是![]() 的中點,BD交AC于點E,過點D作DF∥AC交BA的延長線于點F.
的中點,BD交AC于點E,過點D作DF∥AC交BA的延長線于點F.
(1)求證:DF是⊙O的切線;
(2)若AF=2,FD=4,求tan∠BEC的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
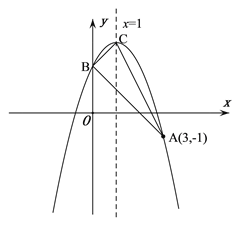
【題目】如圖,拋物線![]() 的頂點為C,對稱軸為直線
的頂點為C,對稱軸為直線![]() ,且經過點A(3,-1),與y軸交于點B.
,且經過點A(3,-1),與y軸交于點B.
(1)求拋物線的解析式;
(2)判斷△ABC的形狀,并說明理由;
(3)經過點A的直線交拋物線于點P,交x軸于點Q,若![]() ,試求出點P的坐標.
,試求出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是用4個全等的直角三角形與1個小正方形鑲嵌而成的正方形圖案.已知大正方形面積為49,小正方形面積為4,若用![]() ,
,![]() 表示直角三角形的兩直角邊
表示直角三角形的兩直角邊![]() ,下列四個說法:①
,下列四個說法:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中說法正確的是
;其中說法正確的是![]()
![]()
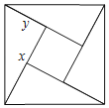
A. ①②B. ①②③C. ①②④D. ①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,OC在∠BOD內.
(1)如果∠AOC和∠BOD都是直角.
①若∠BOC=60°,則∠AOD的度數是 ;
②猜想∠BOC與∠AOD的數量關系,并說明理由;
(2)如果∠AOC=∠BOD=x°,∠AOD=y°,求∠BOC的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
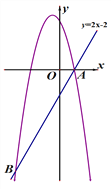
【題目】已知直線y=2x-2與拋物線![]() 交于點A(1,0)和點B,且m<n.
交于點A(1,0)和點B,且m<n.
(1)當m=![]() 時,直接寫出該拋物線頂點的坐標.
時,直接寫出該拋物線頂點的坐標.
(2)求點B的坐標(用含m的代數式表示).
(3)設拋物線頂點為C,記△ABC的面積為S.
①![]() ,求線段AB長度的取值范圍;
,求線段AB長度的取值范圍;
②當![]() 時,求對應的拋物線的函數表達式
時,求對應的拋物線的函數表達式
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com