
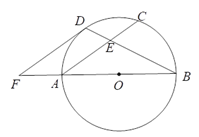
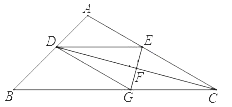
【題目】如圖,AB是⊙O的直徑,C是⊙O上一點,D是![]() 的中點,BD交AC于點E,過點D作DF∥AC交BA的延長線于點F.
的中點,BD交AC于點E,過點D作DF∥AC交BA的延長線于點F.
(1)求證:DF是⊙O的切線;
(2)若AF=2,FD=4,求tan∠BEC的值.
【答案】(1)證明見解析;(2)tan∠BEC=2
【解析】分析:(1)欲證明DF是⊙O的切線,只要證明OD⊥DF ,OD⊥AC
即可。(2)連接AD,在△ODF中利用勾股定理可求出⊙O的半徑,由△ABE∽△FBD可得AE=3,再由△BDA∽△ADE可得![]() ,而∠BEC=∠AED從而即可得出結果。
,而∠BEC=∠AED從而即可得出結果。
本題解析:
(1)證明:連接OD
∵D是![]() 的中點 ∴OD⊥AC
的中點 ∴OD⊥AC
∵DF∥AC ∴OD⊥DF
∵OD為⊙O的半徑 ∴直線AB是⊙O的切線
(2)連接AD,設⊙O的半徑為r,則OD=OA=r,OF=2+r
∵∠ODF=90°, ∴![]() ,解得:r=3,∴AB=6,BF=8
,解得:r=3,∴AB=6,BF=8
∵DF∥AC,∴△ABE∽△FBD, ∴![]() ,即
,即![]() ,∴AE=3
,∴AE=3
∵D是![]() 的中點,∴∠B=∠DAE ,
的中點,∴∠B=∠DAE ,
∵∠BDA=∠ADE,∴△BDA∽△ADE, ∴![]() ,
,
AB是⊙O的直徑, ∴∠ADB=90°, ∴tan∠AED=![]()
∵∠BEC=∠AED,∴tan∠BEC=2


 開心蛙狀元測試卷系列答案
開心蛙狀元測試卷系列答案科目:初中數學 來源: 題型:
【題目】下列圖形都是由相同的小正方形按照一定規律擺放而成,其中第1個圖共有3個小正方形,第2個圖共有8個小正方形,第3個圖共有15個小正方形,第4個圖共有24個小正方形,…,照此規律排列下去,則第8個圖中小正方形的個數是( )
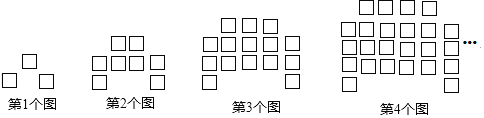
A. 48B. 63C. 80D. 99
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校開展以“迎新年”為主題的藝術活動,舉辦了四個項目的比賽.它們分別是:A演講、B唱歌、C書法、D繪畫.要求每位同學必須參加且限報一項.以九(一)班為樣本進行統計,并將統計結果繪制如下兩幅統計圖,請你結合圖中所給出的信息解答下列問題:
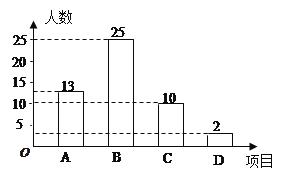
(1)求出參加繪畫比賽的學生人數占全班總人數的百分比;
(2)求出扇形統計圖中參加書法比賽的學生所在的扇形圓心角的度數;

(3)若該校九年級學生共有500人,請你估計這次活動中參加演講和唱歌的學生共有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于a的方程2(a﹣2)=a+4的解也是關于x的方程2(x﹣3)﹣b=7的解.
(1)求a、b的值;
(2)若線段AB=a,在直線AB上取一點P,恰好使![]() =b,點Q為PB的中點,請畫出圖形并求出線段AQ的長.
=b,點Q為PB的中點,請畫出圖形并求出線段AQ的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列兩個等式:![]() ,
,![]() ,給出定義如下:我們稱使等式a﹣b=ab+1的成立的一對有理數a,b為“共生有理數對”,記為(a,b),如:數對
,給出定義如下:我們稱使等式a﹣b=ab+1的成立的一對有理數a,b為“共生有理數對”,記為(a,b),如:數對![]() ,
,![]() ,都是“共生有理數對”.
,都是“共生有理數對”.
(1)數對![]() ,
,![]() 中是“共生有理數對”的是 ;
中是“共生有理數對”的是 ;
(2)若(m,n)是“共生有理數對”,則(﹣n,﹣m) “共生有理數對”(填“是”或“不是”);
(3)請再寫出一對符合條件的“共生有理數對”為 ;(注意:不能與題目中已有的“共生有理數對”重復)
(4)若(a,3)是“共生有理數對”,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2018年6月28日,深湛高鐵正式運營.從湛江到廣州全程約468km,高鐵開通后,運行時間比特快列車所用的時間減少了6h.若高鐵列車的平均速度是特快列車平均速度的3倍,求特快列車與高鐵的平均速度.
查看答案和解析>>
科目:初中數學 來源: 題型:
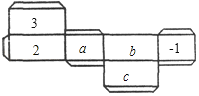
【題目】如圖是一個長方體紙盒的平面展開圖,已知紙盒中相對兩個面上的數互為相反數.
(1)填空:a= ,b= ,c= ;
(2)先化簡,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,CD平分∠ACB,CD的垂直平分線分別交AC、DC、BC
于點E、F、G,連接DE、DG.
(1)求證:四邊形DGCE是菱形;
(2)若∠ACB=30°,∠B=45°,CG=10,求BG的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com