【題目】如圖，在邊長為1的正方形網格中，A(2，4)，B(4，1)，C(-3，4)
(1)平移線段AB到線段CD，使點A與點C重合，寫出點D的坐標．
(2)直接寫出線段AB平移至線段CD處所掃過的面積．
(3)平移線段AB，使其兩端點都在坐標軸上，則點A的坐標為
【答案】（1）(-1，1)；（2）15；（3）(0，3)或(-2，0)
【解析】
（1）根據點A與點C的坐標得出坐標變化規律，從而得到點D的坐標；
（2）根據平移的性質得出ABDC是平行四邊形，根據平行四邊形的面積公式列式計算即可；
（3）分兩種情況：①平移后A的對應點在y軸上，B的對應點在x軸上；②平移后A的對應點在x軸上，B的對應點在y軸上．
(1)∵平移線段AB到線段CD，使點A與點C重合，A(2，4)，C(-3，4)，
∴坐標變化規律是：橫坐標減去5，縱坐標不變，∵B(4，1)，∴點D的坐標為(-1，1)；
(2)∵平移線段AB到線段CD，∴AB∥CD，AB=CD，
∴四邊形ABDC是平行四邊形，∴線段AB平移至線段CD處所掃過的面積為：5×3=15；
(3)分兩種情況：①如果平移后A的對應點在y軸上，B的對應點在x軸上，
那么坐標變化規律是：橫坐標減去2，縱坐標減去1，
∵A(2，4)，∴平移后點A的坐標為(0，3)
②如果平移后A的對應點在x軸上，B的對應點在y軸上，
那么坐標變化規律是：橫坐標減去4，縱坐標減去4，∵A(2，4)，∴平移后點的坐標為(-2，0)；
故答案為(0，3)或(-2，0)．
科目：初中數學 來源： 題型：
【題目】用適當的方法解下列方程．
（1）x2﹣x﹣1=0； （2）x2﹣2x=2x+1；
（3）x（x﹣2）﹣3x2=﹣1； （4）（x+3）2=（1﹣2x）2．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△OAB和△OCD中，OA＝OB，OC＝OD，OA＞OC，∠AOB＝∠COD＝40°，連接AC，BD交于點M，連接OM．下列結論：①AC＝BD；②∠AMB＝40°；③OM平分∠BOC；④MO平分∠BMC．其中正確的是____________________________
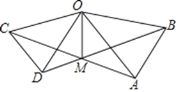
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，點A(
，1)在射線OM上，點B(，3)在射線ON上，以AB為直角邊作Rt△ABA1，以BA1為直角邊作第二個Rt△BA1B1，以A1B1為直角邊作第三個Rt△A1B1A2，…，依此規律，得到Rt△B2018A2019B2019，則點B2019的縱坐標為________.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某廠家新開發的一種摩托車如圖所示，它的大燈
射出的光線
、
與地面
的夾角分別為
和
，大燈離地面距離
．
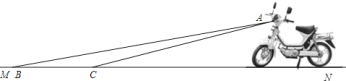
該車大燈照亮地面的寬度
約是多少（不考慮其它因素）？
一般正常人從發現危險到做出剎車動作的反應時間是
，從發現危險到摩托車完全停下所行駛的距離叫做最小安全距離，某人以
的速度駕駛該車，從到摩托車停止的剎車距離是
，請判斷該車大燈的設計是否能滿足最小安全距離的要求，請說明理由．（參考數據：
，
，
，
）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】正方形A1B1C1O，A2B2C2C1，A3B3C3C2…按如圖所示放置，點A1、A2、A3…在直線y=x+1上，點C1、C2、C3…在x軸上，A3的坐標是_____，則An的坐標是_______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示：△ABC是等腰直角三角形，BC=AC，直角頂點C在x軸上，一銳角頂點B在y軸上
(1)如圖1所示，若C的坐標是(2，0)，點A的坐標是(﹣2，﹣2)，求點B的坐標.
(2)如圖2，若y軸恰好平分∠ABC，AC與y軸交于點D，過點A作AE⊥y軸 于E，求證：BD = 2AE
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知拋物線y=ax2+bx+3過等腰Rt△BOC的兩頂點B、C，且與x軸交于點A（﹣1，0）．
（1）求拋物線的解析式；
（2）拋物線的對稱軸與直線BC相交于點M，點N為x軸上一點，當以M，N，B為頂點的三角形與△ABC相似時，求BN的長度；
（3）P為線段BC上方的拋物線上的一個動點，P到直線BC的距離是否存在最大值？若存在，請求出這個最大值的大小以及此時點P的坐標；若不存在，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
