Question

【題目】如圖，在中， ， ， 的高與角平分線相交點，過點作于，交于．下列說法：①；②；③；④；⑤.正確的是_____.

Answer 1

【答案】①③⑤

【解析】（1）∵CH⊥AE于點G，∠ACB=90°，

∴∠CGE=∠ACB=90°，

∴∠BCH+∠CEA=∠CEA+∠CAE=90°，

∴∠CAE=∠BCH；（故說法①成立）

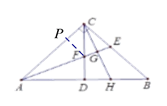
（2）如下圖，連接BF，過點F作FN⊥BC于點N，

∵AB=AC，AD是高，

∴AD平分∠ACB，

又∵AE平分∠BAC，且AE交CD于點F，

∴BF平分∠ABC，

∴DF=NF，

又∵NF<EF，

∴DF<EF；（故說法②錯誤）

（3）∵AC=BC，∠ACB=90°，CD是△ABC的高，

∴∠ACF=∠CBH=45°，

又∵由（1）可知∠CAE=∠BCH，

∴△CAF≌△BCH，

∴CF=BH.

∵∠CAE=∠BAE，∠ACE=∠ADF=90°，

∴∠CEF=∠AFD=∠CFE，

∴CE=CF，

∴CE=BH；（故說法③正確）

（4）如下圖，過點E作EM⊥AB于點M，

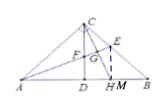
∵AE平分∠BAC，∠ACB=90°，

∴EM=EC，

∵AC=BC，∠ACB=90°，

∴AB=AC，

∵S△ACE=AC·CE，S△ABE=AB·EM，

∴S△ABE=S△ACE；（故說法④錯誤）

（5）如下圖，過點F作FP⊥AC于點P，

∵CD是△ABC的高，AF平分∠BAC，

∴FP=FD，

∴S△ACF ：S△ADF=AC：AD，

∵AC=BC，∠ACB=90°，CD是△ABC的高，

∴AC：AD=，

又∵S△ACF=CF·AD，S△ADF=DF·AD，

∴CF：DF= S△ACF ：S△ADF=AC：AD=，

∴CF=DF；（故說法⑤正確）

綜上所述，正確的說法是①③⑤.

故答案為：①③⑤.