
【題目】已知關(guān)于x的一元二次方程![]() .
.
(1)若方程有兩個(gè)不相等的實(shí)數(shù)根,求k的取值范圍;
(2)當(dāng)k取滿足(1)中條件的最小整數(shù)時(shí),設(shè)方程的兩根為α和β,求代數(shù)式![]() 的值.
的值.
【答案】(1)![]() 且
且![]() ;(2)2020
;(2)2020
【解析】
(1)根據(jù)判別式Δ>0時(shí),一元二次方程有兩個(gè)不相等的實(shí)數(shù)根進(jìn)行求解,即可得到k的取值范圍;
(2)先求出k的最小值,得到![]() ,再根據(jù)根與系數(shù)的關(guān)系得到
,再根據(jù)根與系數(shù)的關(guān)系得到![]() ,
,![]() ,進(jìn)而通過(guò)計(jì)算即可得解.
,進(jìn)而通過(guò)計(jì)算即可得解.
(1)∵方程有兩個(gè)不相等的實(shí)數(shù)根,∴Δ>0,
即![]() ,解不等式得,
,解不等式得,![]() ,
,
又∵![]() 是一元二次方程,
是一元二次方程,
∴![]() ,
,
∴ k的取值范圍是![]() 且
且![]() ;
;
(2)∵k取滿足(1)中條件的最小整數(shù),∴ k的最小整數(shù)值為1,
把k=1代入原方程,得![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
將![]() 兩邊同乘
兩邊同乘![]() ,得
,得![]() ,
,
∴![]()
=![]()
=![]() ,
,
將![]() ,
,![]() 代入得
代入得![]() =
=![]() =2020.
=2020.


 小學(xué)期末標(biāo)準(zhǔn)試卷系列答案
小學(xué)期末標(biāo)準(zhǔn)試卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在![]() 中,已知
中,已知![]() .O是
.O是![]() 上一點(diǎn),
上一點(diǎn),![]() 切
切![]() 于A點(diǎn).
于A點(diǎn).
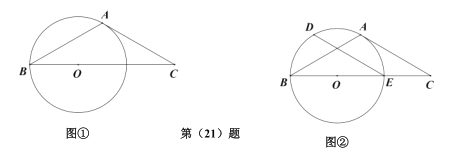
(Ⅰ)如圖①,若![]() 的半徑為6,求線段
的半徑為6,求線段![]() 的長(zhǎng);
的長(zhǎng);
(Ⅱ)如圖②,![]() 交
交![]() 于E點(diǎn),過(guò)E點(diǎn)作
于E點(diǎn),過(guò)E點(diǎn)作![]() 交
交![]() 于點(diǎn)D,若
于點(diǎn)D,若![]() ,求
,求![]() 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,正方形ABCD中,E為CD的中點(diǎn),AE的垂直平分線分別交AD,BC及AB的延長(zhǎng)線于點(diǎn)F,G,H,連接HE,HC,OD,連接CO并延長(zhǎng)交AD于點(diǎn)M.則下列結(jié)論中:
①FG=2AO;②OD∥HE;③![]() ;④2OE2=AHDE;⑤GO+BH=HC
;④2OE2=AHDE;⑤GO+BH=HC
正確結(jié)論的個(gè)數(shù)有( )
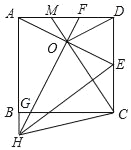
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
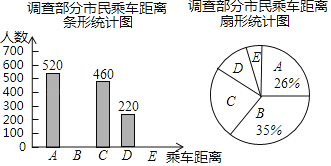
【題目】長(zhǎng)春地鐵一號(hào)線于2017年6月30日正式開(kāi)通.運(yùn)營(yíng)公司根據(jù)乘車(chē)距離制定了不同的票價(jià)類(lèi)別(見(jiàn)對(duì)照表).為了解乘客的乘車(chē)距離,運(yùn)營(yíng)公司隨機(jī)選取了一部分經(jīng)常需要乘車(chē)的市民進(jìn)行了調(diào)查統(tǒng)計(jì),繪制了兩幅不完整的統(tǒng)計(jì)圖.請(qǐng)你根據(jù)圖表中提供的信息解答以下問(wèn)題:
(1)本次抽樣調(diào)查的人數(shù)是_________人.
(2)補(bǔ)全條形統(tǒng)計(jì)圖.
(3)運(yùn)營(yíng)公司估計(jì)這條地鐵專線通車(chē)后每天的客流量約為10萬(wàn)人,請(qǐng)你估算運(yùn)營(yíng)公司的日營(yíng)業(yè)額.
類(lèi)別 | 乘車(chē)距離d(公里) | 票價(jià) |
A | 0<d≤7 | 2 |
B | 7<d≤13 | 3 |
C | 13<d≤19 | 4 |
D | 19<d≤27 | 5 |
E | 27<d≤35 | 6 |
票價(jià)類(lèi)別與乘車(chē)距離對(duì)照表
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,有兩張矩形紙片ABCD和EFGH,AB=EF=2cm,BC=FG=8cm.把紙片ABCD交叉疊放在紙片EFGH上,使重疊部分為平行四邊形,且點(diǎn)D與點(diǎn)G重合.當(dāng)兩張紙片交叉所成的角α最小時(shí),sinα等于( )
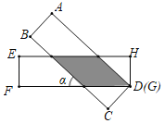
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,點(diǎn)C、A、M、N在同一條直線l上.其中,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,四邊形
,四邊形![]() 為正方形,且
為正方形,且![]() ,將等腰
,將等腰![]() 沿直線l向右平移.若起始位置為點(diǎn)A與點(diǎn)M重合,終止位置為點(diǎn)C與點(diǎn)N重合.設(shè)點(diǎn)A平移的距離為x,兩個(gè)圖形重疊部分的面積為y,則y與x的函數(shù)圖象大致為( )
沿直線l向右平移.若起始位置為點(diǎn)A與點(diǎn)M重合,終止位置為點(diǎn)C與點(diǎn)N重合.設(shè)點(diǎn)A平移的距離為x,兩個(gè)圖形重疊部分的面積為y,則y與x的函數(shù)圖象大致為( )

A.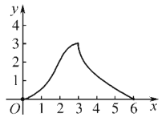 B.
B.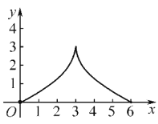
C.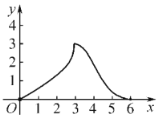 D.
D.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知:![]() 是經(jīng)過(guò)點(diǎn)A的一條直線,點(diǎn)C是直線
是經(jīng)過(guò)點(diǎn)A的一條直線,點(diǎn)C是直線![]() 左側(cè)的一個(gè)動(dòng)點(diǎn),且滿足
左側(cè)的一個(gè)動(dòng)點(diǎn),且滿足![]() ,連接
,連接![]() ,將線段
,將線段![]() 繞點(diǎn)C順時(shí)針旋轉(zhuǎn)60°,得到線段
繞點(diǎn)C順時(shí)針旋轉(zhuǎn)60°,得到線段![]() ,在直線
,在直線![]() 上取一點(diǎn)B,使
上取一點(diǎn)B,使![]() .
.
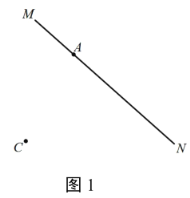
(1)若點(diǎn)C位置如圖1所示.
①依據(jù)題意補(bǔ)全圖1;
②求證:![]() ;
;
(2)連接![]() ,寫(xiě)出一個(gè)
,寫(xiě)出一個(gè)![]() 的值,使得對(duì)于任意一點(diǎn)C,總有
的值,使得對(duì)于任意一點(diǎn)C,總有![]() ,并證明.
,并證明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】新華商場(chǎng)銷(xiāo)售某種冰箱,每臺(tái)進(jìn)貨價(jià)為2500元.市場(chǎng)調(diào)研表明:當(dāng)銷(xiāo)售價(jià)為2900元時(shí),平均每天能售出8臺(tái);而當(dāng)銷(xiāo)售價(jià)每降低50元時(shí),平均每天就能多售出4臺(tái).商場(chǎng)要想使這種冰箱的銷(xiāo)售利潤(rùn)平均每天達(dá)到5000元,設(shè)每臺(tái)冰箱的定價(jià)為x元,則x滿足的關(guān)系式為( )
A. (x2500)(8+4×![]() )=5000 B. (2900x2500)(8+4×
)=5000 B. (2900x2500)(8+4×![]() )=5000
)=5000
C. (x2500)(8+4×![]() )=5000 D. (2900x)(8+4×
)=5000 D. (2900x)(8+4×![]() )=5000
)=5000
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在5×3的網(wǎng)格圖中,每個(gè)小正方形的邊長(zhǎng)均為1,設(shè)經(jīng)過(guò)圖中格點(diǎn)A,C,B三點(diǎn)的圓弧與BD交于E,則圖中陰影部分的面積為____.(結(jié)果保留![]() )
)

查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com