
【題目】如圖,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若點P從點A出發,以每秒1cm的速度沿折線A﹣B﹣C﹣A運動,設運動時間為t(t>0)秒.
(1)AC= cm;
(2)若點P恰好在∠ABC的角平分線上,求此時t的值;
(3)在運動過程中,當t為何值時,△ACP為等腰三角形(直接寫出結果)

【答案】(1)3;(2)t的值為![]() 或5s;(3)當t=
或5s;(3)當t=![]() 或3或
或3或![]() 或6s時,△ACP為等腰三角形.
或6s時,△ACP為等腰三角形.
【解析】
(1)利用勾股定理求解即可;(2)作∠ABC的平分線與AC的交點確定點P,利用全等得PC=PD,再用勾股定理求得PC的長,點P的運動路線長即可求出,由此解得t值(3)分四種情況,找到P點,即可求出t的值.
解:(1)在Rt△ABC中,∠C=90°,AB=5cm,BC=4cm,
∴AC=![]() =3cm.
=3cm.
(2)如圖,過P作PD⊥AB于D,
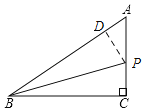
∵BP平分∠ABC,∠C=90°,
∴PD=PC,
又∵BP=BP,
∴Rt△BDP≌Rt△BCP,
∴BD=BC=4,
∴AD=5﹣4=1,
設PD=PC=y,則AP=3﹣y,
在Rt△ADP中,AD2+PD2=AP2,
∴12+y2=(3﹣y)2,
解得y=![]() ,
,
∴CP=![]() ,
,
∴t=5+4+![]() =
=![]() ;
;
當點P與點B重合時,點P也在∠ABC的角平分線上,
此時,t=5;
綜上所述,點P恰好在∠ABC的角平分線上,t的值為![]() 或5s;
或5s;
(3)分四種情況:
①如圖①,當AP=CP時,則∠A=∠ACP,
∵∠A+∠B=900,∠ACP+∠BCP=900,
∴∠B=∠BCP
∴BP=CP=AP
∴AP=![]()
∴ t=![]() ;
;
②如圖②,當AP=AC=3時,t=3;
③當PC=AC=3時,過點C作CD⊥AB于點D,
∵S△ABC=![]() =
=![]() AB
AB![]() CD
CD
∴5CD=12,
∴CD=
∴PD=AD=![]()
∴AP=![]()
∴t=![]() ;
;
④當PC=AC=3時,BP=4-3=1,則AB+BP=5+1=6,∴t=6.
綜上所述,當t=![]() 或3或
或3或![]() 或6s時,△ACP為等腰三角形.
或6s時,△ACP為等腰三角形.


科目:初中數學 來源: 題型:
【題目】如圖,直線AC上取點B,在其同一側作兩個等邊三角形△ABD 和△BCE ,連接AE,CD與GF,下列結論正確的有( )

① AE DC;②AHC120;③△AGB≌△DFB;④BH平分AHC;⑤GF∥AC
A.①②④B.①③⑤C.①③④⑤D.①②③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,花果山上有兩只猴子在一棵樹CD上的點B處,且BC=5m,它們都要到A處吃東西,其中一只猴子甲沿樹爬下走到離樹10m處的池塘A處,另一只猴子乙先爬到樹頂D處后再沿纜繩DA線段滑到A處.已知兩只猴子所經過的路程相等,設BD為xm.
(1)請用含有x的整式表示線段AD的長為______m;
(2)求這棵樹高有多少米?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,二次函數y=ax2﹣2ax﹣3a(a<0)的圖象與x軸交于A、B兩點(點A在點B的右側),與y軸的正半軸交于點C,頂點為D.
(1)求頂點D的坐標(用含a的代數式表示);
(2)若以AD為直徑的圓經過點C.
①求拋物線的函數關系式;
②如圖2,點E是y軸負半軸上一點,連接BE,將△OBE繞平面內某一點旋轉180°,得到△PMN(點P、M、N分別和點O、B、E對應),并且點M、N都在拋物線上,作MF⊥x軸于點F,若線段MF:BF=1:2,求點M、N的坐標;
③點Q在拋物線的對稱軸上,以Q為圓心的圓過A、B兩點,并且和直線CD相切,如圖3,求點Q的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=6,BC=10,AB的垂直平分線分別交BC、AB于點D、E.
(1)求△ACD的周長;
(2)若∠C=25°,求∠CAD的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,長方形ABCD中,AB=5,AD=12,E為AD邊上一點,DE=4,動點P從點B出發,沿B→C→D以2個單位/s作勻速運動,設運動時間為t.
⑴ 當t為 s時,△ABP與△CDE全等;
⑵ 如圖2,EF為△AEP的高,當點P在BC邊上運動時,EF的最小值是 ;
⑶ 當點P在EC的垂直平分線上時,求出t的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:通過小學的學習我們知道,分數可分為“真分數”和“假分數”,而假分數都可化為帶分數,如:![]() 我們定義:在分式中,對于只含有一個字母的分式,當分子的次數大于或等于分母的次數時,我們稱之為“假分式”;當分子的次數小于分母的次數時,我們稱之為“真分式”.
我們定義:在分式中,對于只含有一個字母的分式,當分子的次數大于或等于分母的次數時,我們稱之為“假分式”;當分子的次數小于分母的次數時,我們稱之為“真分式”.
如![]() 這樣的分式就是假分式;再如:
這樣的分式就是假分式;再如:![]() ,
,![]() 這樣的分式就是真分式
這樣的分式就是真分式![]() 類似的,假分式也可以化為帶分式(即:整式與真分式的和的形式)
類似的,假分式也可以化為帶分式(即:整式與真分式的和的形式)
如:![]() ;
;
解決下列問題:
(1)分式![]() 是______分式(填“真分式”或“假分式”);
是______分式(填“真分式”或“假分式”);
(2)將假分式![]() 化為帶分式;
化為帶分式;
(3)如果x為整數,分式![]() 的值為整數,求所有符合條件的x的值.
的值為整數,求所有符合條件的x的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com