
【題目】閱讀材料:
基本不等式![]() ≤
≤![]() (a>0,b>0),當(dāng)且僅當(dāng)a=b時(shí)等號(hào)成立,它是解決最值問(wèn)題的有力工具.
(a>0,b>0),當(dāng)且僅當(dāng)a=b時(shí)等號(hào)成立,它是解決最值問(wèn)題的有力工具.
例如:在x>0的條件下,當(dāng)x為何值時(shí),x+![]() 有最小值,最小值是多少?
有最小值,最小值是多少?
解:∵x>0,![]() >0∴
>0∴![]() ≥
≥![]() ,即
,即![]() ≥2
≥2![]() ,∴
,∴![]() ≥2
≥2
當(dāng)且僅當(dāng)x=![]() ,即x=1時(shí),x+
,即x=1時(shí),x+![]() 有最小值,最小值為2.
有最小值,最小值為2.
請(qǐng)根據(jù)閱讀材料解答下列問(wèn)題:
(1)已知x>0,則當(dāng)x為____時(shí),代數(shù)式3x+![]() 的最小值為______;
的最小值為______;
(2)已知a>0,b>0,a2+b2=7,則ab的最大值為_____
(3)已知矩形面積為9,求矩形周長(zhǎng)的最小值.
【答案】(1)1,6;(2)![]() ;(3)12.
;(3)12.
【解析】
(1)利用基本不等式即可解決問(wèn)題;
(2)利用基本不等式變形式即可得解;
(3)設(shè)這個(gè)矩形的長(zhǎng)為x米,則寬=面積÷長(zhǎng),即寬=![]() 米,則矩形周長(zhǎng)為2倍的長(zhǎng)+2倍的寬,本題就可以轉(zhuǎn)化為兩個(gè)非負(fù)數(shù)的和的問(wèn)題,從而根據(jù)基本不等式求解.
米,則矩形周長(zhǎng)為2倍的長(zhǎng)+2倍的寬,本題就可以轉(zhuǎn)化為兩個(gè)非負(fù)數(shù)的和的問(wèn)題,從而根據(jù)基本不等式求解.
解:(1)∵x>0,3x>0,![]() >0,
>0,
∴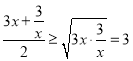 ,
,
即![]() ,
,
當(dāng)且僅當(dāng)3x=![]() ,即x=1時(shí),3x+
,即x=1時(shí),3x+![]() 有最小值,最小值為6.
有最小值,最小值為6.
故答案為:1,6;
(2)由基本不等式![]() ≤
≤![]() (a>0,b>0)得
(a>0,b>0)得
![]()
![]()
即![]() (a>0,b>0)
(a>0,b>0)
當(dāng)且僅當(dāng)a=b時(shí)等號(hào)成立,
∵a2+b2=7,
∴![]()
即![]() ,當(dāng)且僅當(dāng)a=b=
,當(dāng)且僅當(dāng)a=b=![]() 時(shí),等號(hào)成立,
時(shí),等號(hào)成立,
故答案為:![]() ;
;
(3)設(shè)矩形的長(zhǎng)為x米,寬=![]() ,矩形的周長(zhǎng)為2(
,矩形的周長(zhǎng)為2(![]() ),
),
∵x>0,![]() >0,
>0,
∴![]() ,
,
當(dāng)且僅當(dāng)![]() 時(shí)等號(hào)成立,即x=3時(shí),
時(shí)等號(hào)成立,即x=3時(shí),![]() 有最小值6,2(
有最小值6,2(![]() )有最小值12
)有最小值12
即矩形的周長(zhǎng)的最小值為12,此時(shí)長(zhǎng)為3,寬也為3.


 浙大優(yōu)學(xué)小學(xué)年級(jí)銜接捷徑浙江大學(xué)出版社系列答案
浙大優(yōu)學(xué)小學(xué)年級(jí)銜接捷徑浙江大學(xué)出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,△ABC中,E為邊BC延長(zhǎng)線上一點(diǎn),∠ABC的平分線與∠ACE的平分線交于點(diǎn)D,若∠A=46°,則∠D的度數(shù)為( )

A.23°B.92°C.44°D.46°
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】 在平面直角坐標(biāo)系xOy中,O為坐標(biāo)原點(diǎn),四邊形OABC的頂點(diǎn)A在x軸的正半軸上,OA=4,OC=2,點(diǎn)P,點(diǎn)Q分別是邊BC,邊AB上的點(diǎn),連結(jié)AC,PQ,點(diǎn)B1是點(diǎn)B關(guān)于PQ的對(duì)稱點(diǎn).
(1)若四邊形OABC為長(zhǎng)方形,如圖1,
①求點(diǎn)B的坐標(biāo);
②若BQ=BP,且點(diǎn)B1落在AC上,求點(diǎn)B1的坐標(biāo);
(2)若四邊形OABC為平行四邊形,如圖2,且OC⊥AC,過(guò)點(diǎn)B1作B1F∥x軸,與對(duì)角線AC,邊OC分別交于點(diǎn)E,點(diǎn)F.若B1E:B1F=1:3,點(diǎn)B1的橫坐標(biāo)為m,求點(diǎn)B1的縱坐標(biāo)(用含m的代數(shù)式表示).

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
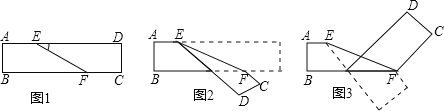
【題目】如圖1是長(zhǎng)方形紙袋,將紙袋沿EF折疊成圖2,再沿BF折疊成圖3,若∠DEF=α,用α表示圖3中∠CFE的大小為 _________ .
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知線段AB,A(2,1),B(4,3),現(xiàn)將線段AB沿y軸方向向下平移得到線段MN,直線y=mx+b過(guò)M、N兩點(diǎn),且M、N兩點(diǎn)恰好也落在雙曲線y=![]() 的一條分支上,
的一條分支上,

(1)求反比例函數(shù)和一次函數(shù)的解析式.
(2)直接寫出不等式mx+b-![]() ≥0的解集
≥0的解集
(3)若點(diǎn)C(x1,a),D(x2,a-1)在雙曲線y=![]() 上,試比較x1和x2的大小.
上,試比較x1和x2的大小.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知:反比例函數(shù)![]() 的圖像過(guò)點(diǎn)A(
的圖像過(guò)點(diǎn)A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() )且
)且![]()
(1)求m的值;
(2)點(diǎn)C在x軸上,且![]() ,求C點(diǎn)的坐標(biāo);
,求C點(diǎn)的坐標(biāo);
(3)點(diǎn)Q是第一象限內(nèi)反比例函數(shù)圖象上的動(dòng)點(diǎn),且在直線AB的右側(cè),設(shè)直線QA,QB與y軸分別交于點(diǎn)E、D,試判斷DE的長(zhǎng)度是否變化,若變化請(qǐng)說(shuō)明理由,若不變,請(qǐng)求出長(zhǎng)度.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某市為了鼓勵(lì)居民節(jié)約用水,決定實(shí)行兩級(jí)收費(fèi)制度.若每月用水量不超過(guò)14噸,則每噸按政府補(bǔ)貼優(yōu)惠價(jià)a元收費(fèi);若每月用水量超過(guò)14噸,則超過(guò)部分每噸按市場(chǎng)調(diào)節(jié)價(jià)b元收費(fèi).小劉家3月份用水10噸,交水費(fèi)20元;4月份用水16噸,交水費(fèi)35元.
(1)求每噸水的政府補(bǔ)貼優(yōu)惠價(jià)和市場(chǎng)調(diào)節(jié)價(jià)分別是多少?
(2)設(shè)每月用水量為x噸,應(yīng)交水費(fèi)為y元,請(qǐng)寫出y與x之間的函數(shù)關(guān)系式;
(3)小劉預(yù)計(jì)他家5月份用水不會(huì)超過(guò)22噸,那么小劉家5月份最多交多少元水費(fèi)?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在“綠滿鄂南”行動(dòng)中,某社區(qū)計(jì)劃對(duì)面積為1800m2的區(qū)域進(jìn)行綠化.經(jīng)投標(biāo),由甲、乙兩個(gè)工程隊(duì)來(lái)完成,已知甲隊(duì)每天能完成綠化的面積是乙隊(duì)每天能完成綠化面積的2倍,并且在獨(dú)立完成面積為400m2區(qū)域的綠化時(shí),甲隊(duì)比乙隊(duì)少用4天.
(1)求甲、乙兩工程隊(duì)每天能完成綠化的面積.
(2)設(shè)甲工程隊(duì)施工x天,乙工程隊(duì)施工y天,剛好完成綠化任務(wù),求y與x的函數(shù)解析式.
(3)若甲隊(duì)每天綠化費(fèi)用是0.6萬(wàn)元,乙隊(duì)每天綠化費(fèi)用為0.25萬(wàn)元,且甲乙兩隊(duì)施工的總天數(shù)不超過(guò)26天,則如何安排甲乙兩隊(duì)施工的天數(shù),使施工總費(fèi)用最低?并求出最低費(fèi)用.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知:∠MON=30°,點(diǎn)A1、A2、A3…在射線ON上,點(diǎn)B1、B2、B3…在射線OM上,△A1B1A2、△A2B2A3、△A3B3A4…均為等邊三角形,若OA1=1,則△A5B5A6的邊長(zhǎng)為( )

A.6B.16C.32D.64
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com