
【題目】(題文)如圖,已知拋物線![]() 經過
經過![]() ,
,![]() 兩點,頂點為
兩點,頂點為![]() .
.
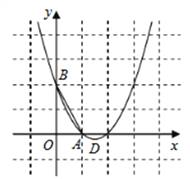
(1)求拋物線的解析式;
(2)將![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 后,點
后,點![]() 落在點
落在點![]() 的位置,將拋物線沿
的位置,將拋物線沿![]() 軸平移后經過點
軸平移后經過點![]() ,求平移后所得圖象的函數關系式;
,求平移后所得圖象的函數關系式;
(3)設(2)中平移后,所得拋物線與![]() 軸的交點為
軸的交點為![]() ,頂點為
,頂點為![]() ,若點
,若點![]() 在平移后的拋物線上,且滿足
在平移后的拋物線上,且滿足![]() 的面積是
的面積是![]() 面積的2倍,求點
面積的2倍,求點![]() 的坐標.
的坐標.
【答案】(1)拋物線的解析式為![]() .(2)平移后的拋物線解析式為:
.(2)平移后的拋物線解析式為:![]() .(3)點
.(3)點![]() 的坐標為
的坐標為![]() 或
或![]() .
.
【解析】(1)利用待定系數法,將點A,B的坐標代入解析式即可求得;
(2)根據旋轉的知識可得:A(1,0),B(0,2),∴OA=1,OB=2,
可得旋轉后C點的坐標為(3,1),當x=3時,由y=x2-3x+2得y=2,可知拋物線y=x2-3x+2過點(3,2)∴將原拋物線沿y軸向下平移1個單位后過點C.∴平移后的拋物線解析式為:y=x2-3x+1;
(3)首先求得B1,D1的坐標,根據圖形分別求得即可,要注意利用方程思想.
詳解: (1)已知拋物線![]() 經過
經過![]() ,
,![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴所求拋物線的解析式為![]() .
.
(2)∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
可得旋轉后![]() 點的坐標為
點的坐標為![]() .
.
當![]() 時,由
時,由![]() 得
得![]() ,
,
可知拋物線![]() 過點
過點![]() .
.
∴將原拋物線沿![]() 軸向下平移1個單位長度后過點
軸向下平移1個單位長度后過點![]() .
.
∴平移后的拋物線解析式為:![]() .
.
(3)∵點![]() 在
在![]() 上,可設
上,可設![]() 點坐標為
點坐標為![]() ,
,
將![]() 配方得
配方得![]() ,∴其對稱軸為
,∴其對稱軸為![]() .由題得B1(0,1).
.由題得B1(0,1).
①當![]() 時,如圖①,
時,如圖①,
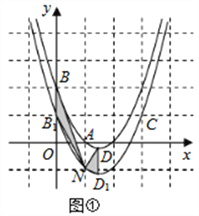
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
此時![]() ,
,
∴![]() 點的坐標為
點的坐標為![]() .
.
②當![]() 時,如圖②,
時,如圖②,
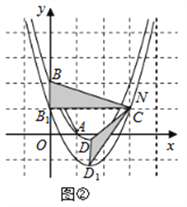
同理可得![]() ,
,
∴![]() ,
,
此時![]() ,
,
∴![]() 點的坐標為
點的坐標為![]() .
.
綜上,點![]() 的坐標為
的坐標為![]() 或
或![]() .
.


 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】由我國完全自主設計、自主建造的首艘國產航母于2018年5月成功完成第一次海上試驗任務.如圖,航母由西向東航行,到達![]() 處時,測得小島
處時,測得小島![]() 位于它的北偏東
位于它的北偏東![]() 方向,且與航母相距80海里,再航行一段時間后到達B處,測得小島
方向,且與航母相距80海里,再航行一段時間后到達B處,測得小島![]() 位于它的北偏東
位于它的北偏東![]() 方向.如果航母繼續航行至小島
方向.如果航母繼續航行至小島![]() 的正南方向的
的正南方向的![]() 處,求還需航行的距離
處,求還需航行的距離![]() 的長.
的長.
(參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用直尺和圓規畫一個角等于已知角,是運用了“全等三角形的對應角相等”這一性質,其全等的依據是( )
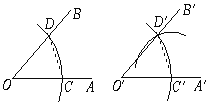
A.SAS B.ASA C.AAS D.SSS
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列所給條件中,不能判斷兩個直角三角形全等的是( )
A. 一個銳角和這個銳角的對邊對應相等B. 一個銳角與斜邊對應相等
C. 兩銳角對應相等D. 一銳角和一邊對應相等
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點C是線段AB的中點,延長線段AB至點D,使BD=AB,延長AD至點E,使DE=AC.
![]()
(1)依題意畫出圖形(尺規作圖),則![]() =_________(直接寫出結果);
=_________(直接寫出結果);
(2)若DE=3,求AB的長;
(3)請寫出與BE長度相同的線段.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在⊙O中,AB是⊙O的直徑,AB=10,![]() ,點E是點D關于AB的對稱點,M是AB上的一動點,下列結論:①∠BOE=60°;②∠CED=
,點E是點D關于AB的對稱點,M是AB上的一動點,下列結論:①∠BOE=60°;②∠CED=![]() ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述結論中正確的個數是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述結論中正確的個數是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】
![]()
(1)OA= cm,OB= cm.
(2)若點C是線段AO上一點,且滿足AC=CO+CB,求CO的長.
(3)若動點P、Q分別從A、B同時出發,向右運動,點P的速度為2cm/s,點Q的速度為1cm/s,設運動時間為t(s),當點P與點Q重合時,P、Q兩點停止運動.
①當t為何值時,2OP﹣OQ=8.
②當點P經過點O時,動點M從點O出發,以3cm/s的速度也向右運動.當點M追上點Q后立即返回,以同樣的速度向點P運動,遇到點P后立即返回,又以同樣的速度向點Q運動,如此往返,直到點P、Q停止時,點M也停止運動.在此過程中,點M行駛的總路程為 cm.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com