【題目】在△ABC中，∠B=45°，點D在邊BC上，AD=AC，點E在邊AD上，∠BCE=45°，若AB=5 
．AE=2DE，則AC= ． 
【答案】
【解析】解：過A作AM⊥BC于M，過作EN∥AB交BC于N，
則△DEN∽△DAB，∴∠ENC=∠B=45°，
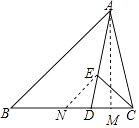
∴△ABM與△ENC是等腰直角三角形，
∵AB=5 
，
∴AM=BM=5，
∵DE：AE= 
，
∴ 
= 
，
∴ 
= ，
∴NE= 
，
∴NC= 
，
設CM=x，則CD=2x，ND=NC﹣CD= ﹣2x，BO=5﹣x，
則 
= ，
即 
= ，
∴x=1，∴CM=1，
∴AC= 
= ．
所以答案是： ．
【考點精析】掌握相似三角形的判定與性質是解答本題的根本，需要知道相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等）的比等于相似比；相似三角形周長的比等于相似比；相似三角形面積的比等于相似比的平方．
科目：初中數學 來源： 題型：
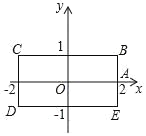
【題目】如圖，長方形 BCDE 的各邊分別平行于 x 軸或 y 軸，物體甲和物體乙分別由點 A（2，0）同時出發，沿長方形 BCDE 的邊作環繞運動，物體甲按逆時針方向以 1 個單位/秒勻速運動，物體乙按順時針方向以 2 個單位/秒勻速運動，則兩個物體運動后的第 2020 次相遇地點的坐標是_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知拋物線l1：y=﹣x2+2x+3與x軸交于點A，B（點A在點B左邊），與y軸交于點C，拋物線l2經過點A，與x軸的另一個交點為E（4，0），與y軸交于點D（0，﹣2）．
（1）求拋物線l2的解析式；
（2）點P為線段AB上一動點（不與A、B重合），過點P作y軸的平行線交拋物線l1于點M，交拋物線l2于點N．
①當四邊形AMBN的面積最大時，求點P的坐標；
②當CM=DN≠0時，求點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
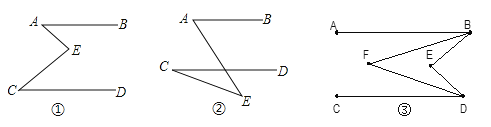
【題目】（1）如圖①、②，AB∥CD，你能說明∠A、∠E、∠C的關系嗎？（請在圖形下的橫線上寫出其關系并選一個進行說明）
（2）如圖③若AB∥CD，BF平分∠ABE，DF平分∠CDE，∠BED=80，則∠BFD=________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△DEF是△ABC經過平移得到的．已知∠A=54°，∠ABC=36°，則下列結論不一定成立的是( )
A. ∠F=90° B. ∠BED=∠FED C. BC⊥DF D. DF∥AC
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，將方格紙中的△ABC向上平移4個單位長度，然后向右平移6個單位長度，得到△A1B1C1．
（1）畫出平移后的圖形；
（2）線段AA1，BB1的位置關系是______；數量關系是________.
（3）如果每個方格的邊長是1，那么△ABC的面積是___．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一家商店進行門店升級需要裝修，裝修期間暫停營業，若請甲乙兩個裝修組同時施工，8天可以完成，需付費用共3520元；若先請甲組單獨做6天，再請乙組單獨做12天可以完成，需付費用3480元，問：
（1）甲、乙兩組工作一天，商店各應付多少錢？
（2）已知甲組單獨完成需12天，乙組單獨完成需24天，單獨請哪個組，商店所需費用最少？
（3）裝修完畢第二天即可正常營業，且每天仍可盈利200元(即裝修前后每天盈利不變)，你認為商店應如何安排施工更有利？說說你的理由．(可用（1）（2）問的條件及結論)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，把八個等圓按相鄰兩兩外切擺放，其圓心連線構成一個正八邊形，設正八邊形內側八個扇形（無陰影部分）面積之和為S1 ， 正八邊形外側八個扇形（陰影部分）面積之和為S2 ， 則 
=（ ）
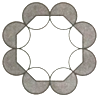
A.
B.
C.
D.1
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一次函數y=kx+b的圖象分別與反比例函數y= 
的圖象在第一象限交于點A（4，3），與y軸的負半軸交于點B，且OA=OB．
（1）求函數y=kx+b和y= 的表達式；
（2）已知點C（0，5），試在該一次函數圖象上確定一點M，使得MB=MC，求此時點M的坐標．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com