
【題目】(綜合與實踐
如圖,直線![]() 的函數(shù)關(guān)系式為
的函數(shù)關(guān)系式為![]() ,且
,且![]() 與
與![]() 軸交于點A,直線
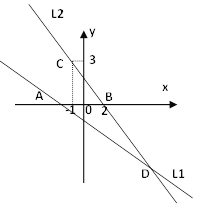
軸交于點A,直線![]() 經(jīng)過點B(2,0),C(-1,3),直線
經(jīng)過點B(2,0),C(-1,3),直線![]() 與
與![]() 交于點D.
交于點D.
(1)求直線![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)求△ABD的面積.
(3)點P是![]() 軸上一動點,問是否存在一點P,恰好使△ADP為直角三角形?若存在,直接寫出點P的坐標(biāo);若不存在,請說明理由.
軸上一動點,問是否存在一點P,恰好使△ADP為直角三角形?若存在,直接寫出點P的坐標(biāo);若不存在,請說明理由.
【答案】(1)y=-x+2;(2)8;(3)存在,點P的坐標(biāo)為(6,0)或(8,0)
【解析】
(1)根據(jù)直線l2經(jīng)過點A(2,0),B(-1,3),可以求得直線l2的函數(shù)關(guān)系式;
(2)將直線l1和直線l2的函數(shù)表達(dá)式聯(lián)立成二元一次方程組,即可求得點D的坐標(biāo);根據(jù)直線l1的表達(dá)式可以求得點A的坐標(biāo),即可求得△ABD的面積.
(3)分∠APD=90°時、∠ADP=90°時兩種情況討論.
(1)設(shè)直線l2的函數(shù)關(guān)系式為:y=kx+b,
∵直線過點B(2,0),C(-1,3),
∴![]()
解得:![]() ,
,
∴直線l2的函數(shù)關(guān)系式為:y=-x+2;
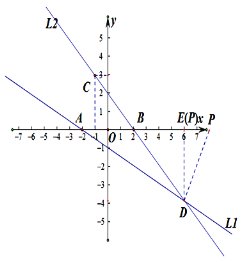
(2)過點D作DE⊥x軸,垂足為點E
∵直線l1與l2交于點D.
∴ ,解得
,解得![]() ,
,
∴ D(6,-4)
∴DE=4
將y=0代入y=-![]() x-1得x=-2,
x-1得x=-2,
∴點A的坐標(biāo)是(-2,0),
∵點B的坐標(biāo)是(2,0),
∴AB=4..
∴S△ABC=![]() AB×DE=
AB×DE=![]() ×4×4=8.
×4×4=8.
(3)存在一點P,恰好使△ADP為直角三角形, 點P的坐標(biāo)為(6,0)或(8,0). 理由是:
當(dāng)∠APD=90°時,P1點坐標(biāo)為(6,0)
當(dāng)∠ADP=90°時,設(shè)P(x,0)
可列方程為:42+(x-6)2=(x+2)2-(42+82)
解得:x=8
所以P(8,0)
∴點P的坐標(biāo)為(6,0)或(8,0)


科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知二次函數(shù)y=x2+mx+n的圖象經(jīng)過A(0,3),且對稱軸是直線x=2.
(1)求該函數(shù)的解析式;
(2)在拋物線上找一點P,使△PBC的面積是△ABC的面積的![]() ,求出點P的坐標(biāo).
,求出點P的坐標(biāo).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】材料一:我們可以將任意三位數(shù)記為![]() ,(其中
,(其中![]() 、
、![]() 、
、![]() 分別表示該數(shù)的百位數(shù)字,十位數(shù)字和個位數(shù)字,且
分別表示該數(shù)的百位數(shù)字,十位數(shù)字和個位數(shù)字,且![]() ),顯然
),顯然![]() .
.
材料二:若一個三位數(shù)的百位數(shù)字,十位數(shù)字和個位數(shù)字均不為0,則稱之為初始數(shù),比如123就是一個初始數(shù),將初始數(shù)的三個數(shù)位上的數(shù)字交換順序,可產(chǎn)生出5個新的初始數(shù),比如由123可以產(chǎn)生出132,213,231,312,321這5個新初始數(shù),這6個初始數(shù)的和成為終止數(shù).
(1)求初始數(shù)125生成的終止數(shù);
(2)若一個初始數(shù)![]() ,滿足
,滿足![]() ,且
,且![]() ,記
,記![]() ,
,![]() ,
,![]() ,若
,若![]() ,求滿足條件的初始數(shù)的值.
,求滿足條件的初始數(shù)的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】2020年是全面建成小康社會收官之年,某扶貧幫扶小組積極響應(yīng),對農(nóng)民實施精準(zhǔn)扶貧.某農(nóng)戶老張家種植花椒和黑木耳兩種干貨共800千克,扶貧小組通過市場調(diào)研發(fā)現(xiàn),花椒市場價60元/千克,黑木耳市場價48元/千克,老張全部售完可以收入4.2萬元.已知老張種植花椒成本需25元/千克,種植木耳成本需35元/千克,根據(jù)脫貧目標(biāo)任務(wù)要求,老張種植花椒和黑木耳的兩種干貨的純收入(銷售收入-種植成本)在2萬元以上才可以順利脫貧.請你分析一下扶貧幫扶小組是否能幫助老張順利脫貧.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】風(fēng)電已成為我國繼煤電、水電之后的第三大電源,風(fēng)電機(jī)組主要由塔桿和葉片組成(如圖①),圖②是平面圖.光明中學(xué)的數(shù)學(xué)興趣小組針對風(fēng)電塔桿進(jìn)行了測量,甲同學(xué)站在平地上的A處測得塔桿頂端C的仰角是55°,乙同學(xué)站在巖石B處測得葉片的最高位置D的仰角是45°(D,C,H在同一直線上,G,A,H在同一條直線上),他們事先從相關(guān)部門了解到葉片的長度為15米(塔桿與葉片連接處的長度忽略不計),巖石高BG為4米,兩處的水平距離AG為23米,BG⊥GH,CH⊥AH,求塔桿CH的高.(參考數(shù)據(jù):tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】隨著人們“節(jié)能環(huán)保,綠色出行”意識的增強(qiáng),越來越多的人喜歡騎自行車出行,同時也給自行車商家?guī)砩虣C(jī). 某自行車行銷售![]() 型,
型,![]() 型兩種自行車,經(jīng)統(tǒng)計,2019年此車行銷售這兩種自行車情況如下:
型兩種自行車,經(jīng)統(tǒng)計,2019年此車行銷售這兩種自行車情況如下:![]() 自行車銷售總額為8萬元. 每輛
自行車銷售總額為8萬元. 每輛![]() 型自行車的售價比每輛
型自行車的售價比每輛![]() 型自行車的售價少200元,
型自行車的售價少200元,![]() 型自行車銷售數(shù)量是
型自行車銷售數(shù)量是![]() 自行車的1. 25倍,
自行車的1. 25倍, ![]() 自行車銷售總額比A型自行車銷售總額多
自行車銷售總額比A型自行車銷售總額多![]() .
.
(1)求每輛![]() 型自行車的售價多少元.
型自行車的售價多少元.
(2)若每輛![]() 型自行車進(jìn)價1400元,每輛
型自行車進(jìn)價1400元,每輛![]() 型自行車進(jìn)價1300元,求此自行車行2019年銷售
型自行車進(jìn)價1300元,求此自行車行2019年銷售![]() 型自行車的總利潤.
型自行車的總利潤.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
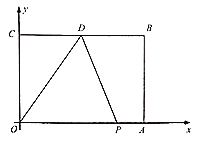
【題目】如圖,在平面直角坐標(biāo)系中,長方形![]() 的頂點
的頂點![]() 的坐標(biāo)分別為
的坐標(biāo)分別為![]() ,
,![]() ,
,![]() 是
是![]() 的中點,動點
的中點,動點![]() 從
從![]() 點出發(fā),以每秒
點出發(fā),以每秒![]() 個單位長度的速度,沿著
個單位長度的速度,沿著![]() 運動,設(shè)點
運動,設(shè)點![]() 運動的時間為
運動的時間為![]() 秒(
秒(![]() ).
).
(1)點![]() 的坐標(biāo)是______;
的坐標(biāo)是______;
(2)當(dāng)點![]() 在
在![]() 上運動時,點
上運動時,點![]() 的坐標(biāo)是______(用
的坐標(biāo)是______(用![]() 表示);
表示);
(3)求![]() 的面積
的面積![]() 與
與![]() 之間的函數(shù)表達(dá)式,并寫出對應(yīng)自變量
之間的函數(shù)表達(dá)式,并寫出對應(yīng)自變量![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
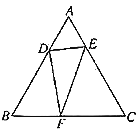
【題目】如圖,![]() 是等邊三角形,
是等邊三角形,![]() ,點
,點![]() 、
、![]() 分別為邊
分別為邊![]() 、
、![]() 上的動點,當(dāng)
上的動點,當(dāng)![]() 的周長最小時,
的周長最小時,![]() 的度數(shù)是______________.
的度數(shù)是______________.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com