
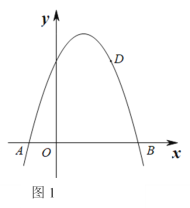
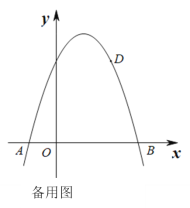
【題目】如圖1,拋物線y=ax2+bx +3與x軸的交點為A和B,其中點A(-1,0),且點D(2,3)在該拋物線上.
(1)求該拋物線所對應的函數解析式;
(2)點P是線段AB上的動點(點P不與點A,B重合),過點P作PQ⊥x軸交該拋物線于點Q,連接AQ,DQ,記點P的橫坐標為t.
①若![]() 時,求△
時,求△![]() 面積的最大值;
面積的最大值;
②若△![]() 是以Q為直角頂點的直角三角形時,求所有滿足條件的點Q的坐標.
是以Q為直角頂點的直角三角形時,求所有滿足條件的點Q的坐標.
【答案】(1)![]() ;(2)①當
;(2)①當![]() 時,△ADQ面積最大為
時,△ADQ面積最大為![]() ;②Q(
;②Q(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)把A(-1,0),D(2,3)代入解析式即可求解;
(2)①由P的橫坐標為t, Q(t,![]() ),求出直線AD的解析式為
),求出直線AD的解析式為![]() ,設點C為直線PQ與直線AD的交點,求得點
,設點C為直線PQ與直線AD的交點,求得點![]() 坐標為(
坐標為(![]() ),得到
),得到![]()
![]() ,利用
,利用![]() ,將△
,將△![]() 面積表示為關于t的二次函數,故可求解;
面積表示為關于t的二次函數,故可求解;
②△AQD是以Q為直角頂點的直角三角形時,∠AQD=90°,過點D作DK⊥PQ于點K,
證明△PQA∽△KDQ得到![]() ,代入得
,代入得![]() ,解出t即可求解.
,解出t即可求解.
(1)解:將A(-1,0)和點D(2,3)代入![]() 得,
得,
![]() ,
,
解得![]() ,
,
∴該拋物線的解析式為![]() .
.
(2)①由P的橫坐標為t,則P(t,0),Q(t,![]() ).
).
設直線AD的解析式為y=kx+b(k≠0)
把A(-1,0),D(2,3)代入得![]()
解得![]()
∴直線AD的解析式為![]()
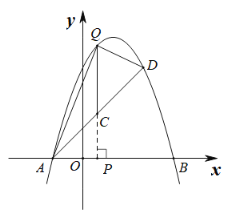
如圖:設點C為直線PQ與直線AD的交點
當![]() 時,
時,![]()
∴點![]() 坐標為(
坐標為(![]() )
)
∴![]()
![]()
∴![]()
![]()
![]()
![]()
![]()
![]()
![]() 拋物線開口向下
拋物線開口向下
∴當![]() 時,△ADQ面積最大為
時,△ADQ面積最大為![]() ;
;
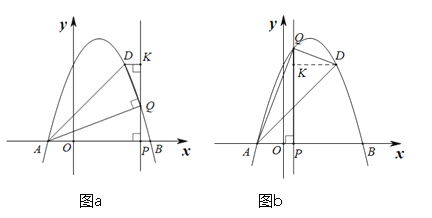
②△AQD是以Q為直角頂點的直角三角形時,∠AQD=90°,
過點D作DK⊥PQ于點K,
∴∠APQ=∠QKD=90°,
∵∠DQK+∠PQA=90°,
又∠DQK+∠KDQ=90°,
∴∠PQA=∠KDQ,
∴△PQA∽△KDQ
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() (即Q不與A、D重合),
(即Q不與A、D重合),
∴![]() ,整理得:
,整理得:![]() ,
,
解得![]() ,
,![]()
經驗證,![]() 、
、![]() 均符合題意,
均符合題意,
其中:![]() ,符合圖a的情況,
,符合圖a的情況,![]() ,符合圖b的情況.
,符合圖b的情況.
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
∴Q(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中數學 來源: 題型:
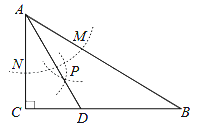
【題目】如圖,在△ABC中,∠C=90°,∠B=32°,以A為圓心,任意長為半徑畫弧分別交AB,AC于點M和N,再分別以M,N為圓心,大于![]() MN的長為半徑畫弧,兩弧交于點P,連接AP并延長交BC于點D,則下列說法:
MN的長為半徑畫弧,兩弧交于點P,連接AP并延長交BC于點D,則下列說法:
①AD是∠BAC的平分線;
②CD是△ADC的高;
③點D在AB的垂直平分線上;
④∠ADC=61°.
其中正確的有( ).
A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某校初二學生每周上網的時間,兩位學生進行了抽樣調查.小麗調查了初二電腦愛好者中40名學生每周上網的時間;小杰從全校400名初二學生中隨機抽取了40名學生,調查了每周上網的時間.小麗與小杰整理各自樣本數據,如下表所示:
時間段 (小時/周) | 小麗抽樣 人數 | 小杰抽樣 人數 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(每組可含最低值,不含最高值)
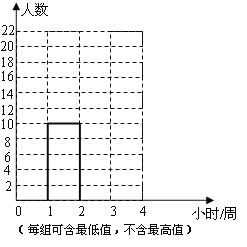
(1)你認為哪位同學抽取的樣本不合理?請說明理由;
(2)根據合理抽取的樣本,把上圖中的頻數分布直方圖補畫完整;
(3)專家建議每周上網2小時以上(含2小時)的同學應適當減少上網的時間,估計該校全體初二學生中有多少名同學應適當減少上網的時間?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著經濟的快速發展,環境問題越來越受到人們的關注.某校學生會為了了解垃圾分類知識的普及情況,隨機調查了部分學生,調查結果分為“非常了解”“了解”“了解較少”“不了解”四類,并將調查結果繪制成下面兩幅統計圖.

(1)求:本次被調查的學生有多少名?補全條形統計圖.
(2)估計該校1200名學生中“非常了解”與“了解”的人數和是多少.
(3)被調查的“非常了解”的學生中有2名男生,其余為女生,從中隨機抽取2人在全校做垃圾分類知識交流,請利用畫樹狀圖或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 如圖,在△ABC中,DE是邊AB的垂直平分線,分別交邊AB,AC于點D,E,連接BE,點F在邊AC上,AB=AF,連接BF.
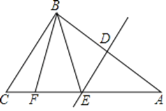
(1)求證:∠BEC=2∠A;
(2)當∠BFC=108°時,求∠A的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場舉辦抽獎活動,規則如下:在不透明的袋子中有2個黑球和2個紅球,這些球除顏色外都相同.顧客每次摸出一個球,若摸到黑球,則獲得1份獎品;若摸到紅球,則沒有獎品.
(1)如果小芳只有一次摸球機會,那么小芳獲得獎品的概率為 ;
(2)如果小芳有兩次摸球機會(摸出后不放回),求小芳獲得2份獎品的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a<0)的圖象與x軸的兩個交點A、B的橫坐標分別為﹣3、1,與y軸交于點C,下面四個結論:
①16a+4b+c>0:
②若P(﹣5,y1),Q(![]() ,y2)是函數圖象上的兩點,則y1<y2;
,y2)是函數圖象上的兩點,則y1<y2;
③c=3a;
④若△ABC是等腰三角形,則b=﹣![]() 或﹣
或﹣![]() .
.
其中正確的有_____.(請將正確結論的序號全部填在橫線上)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com