
【題目】 如圖,在△ABC中,DE是邊AB的垂直平分線,分別交邊AB,AC于點D,E,連接BE,點F在邊AC上,AB=AF,連接BF.
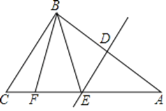
(1)求證:∠BEC=2∠A;
(2)當∠BFC=108°時,求∠A的度數.
 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案科目:初中數學 來源: 題型:
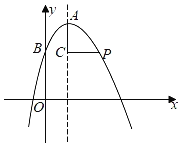
【題目】如圖,在平面直角坐標系xOy中,已知拋物線的頂點為A(2,![]() ),拋線物與y軸交于點B(0,
),拋線物與y軸交于點B(0,![]() ),點C在其對稱軸上且位于點A下方,將線段AC繞點C按順時針方向旋轉90°,點A落在拋物線上的點P處.
),點C在其對稱軸上且位于點A下方,將線段AC繞點C按順時針方向旋轉90°,點A落在拋物線上的點P處.
(1)求拋物線的解析式;
(2)求線段AC的長;
(3)將拋物線平移,使其頂點A移到原點O的位置,這時點P落在點D的位置,如果點M在y軸上,且以O,C,D,M為頂點的四邊形的面積為8,求點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
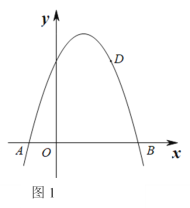
【題目】如圖1,拋物線y=ax2+bx +3與x軸的交點為A和B,其中點A(-1,0),且點D(2,3)在該拋物線上.
(1)求該拋物線所對應的函數解析式;
(2)點P是線段AB上的動點(點P不與點A,B重合),過點P作PQ⊥x軸交該拋物線于點Q,連接AQ,DQ,記點P的橫坐標為t.
①若![]() 時,求△
時,求△![]() 面積的最大值;
面積的最大值;
②若△![]() 是以Q為直角頂點的直角三角形時,求所有滿足條件的點Q的坐標.
是以Q為直角頂點的直角三角形時,求所有滿足條件的點Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某花店用3600元按批發價購買了一批花卉.若將批發價降低10%,則可以多購買該花卉20盆.市場調查反映,該花卉每盆售價25元時,每天可賣出25盆.若調整價格,每盆花卉每漲價1元,每天要少賣出1盆.
(1)該花卉每盆批發價是多少元?
(2)若每天所得的銷售利潤為200元時,且銷量盡可能大,該花卉每盆售價是多少元?
(3)為了讓利給顧客,該花店決定每盆花卉漲價不超過5元,問該花卉一天最大的銷售利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 如圖,在平面直角坐標系中,點A的坐標為(6,![]() ),AB⊥x軸于點B,AC⊥y軸于點C,連接BC.點D是線段AC的中點,點E的坐標為(0,
),AB⊥x軸于點B,AC⊥y軸于點C,連接BC.點D是線段AC的中點,點E的坐標為(0,![]() ),點F是線段EO上的一個動點.過點A,D,F的拋物線與x軸正半軸交于點G,連接DG交線段AB于點M.
),點F是線段EO上的一個動點.過點A,D,F的拋物線與x軸正半軸交于點G,連接DG交線段AB于點M.
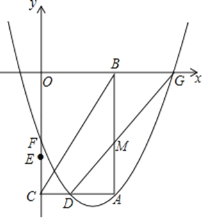
(1)求∠ACB的度數;
(2)當點F運動到原點時,求過A,D,F三點的拋物線的函數表達式及點G的坐標;
(3)以線段DM為一邊作等邊三角形DMP,點P與點A在直線DG同側,當點F從點E運動到點O時,請直接寫出點P運動的路徑的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
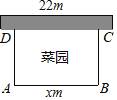
【題目】如圖,用一段長為30m的籬笆圍成一個一邊靠墻的矩形菜園(矩形ABCD),墻長為22m,這個矩形的長AB=xm,菜園的面積為Sm2,且AB>AD.
(1)求S與x之間的函數關系式,并寫出自變量x的取值范圍.
(2)若要圍建的菜園為100m2時,求該萊園的長.
(3)當該菜園的長為多少m時,菜園的面積最大?最大面積是多少m2?
查看答案和解析>>
科目:初中數學 來源: 題型:
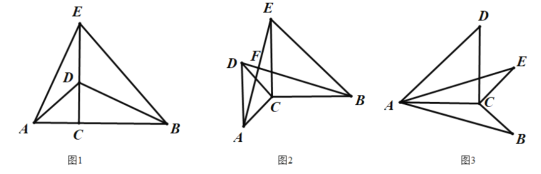
【題目】(1)問題發現:如圖1,已知點![]() 為線段
為線段![]() 上一點,分別以線段
上一點,分別以線段![]() 為直角邊作兩個等腰直角三角形,
為直角邊作兩個等腰直角三角形,![]() ,連接
,連接![]() ,線段
,線段![]() 之間的數量關系為__;位置關系為_________.
之間的數量關系為__;位置關系為_________.
(2)拓展研究:如圖2,把![]() 繞點C逆時針旋轉,線段
繞點C逆時針旋轉,線段![]() 交于點F,則
交于點F,則![]() 之間的關系是否仍然成立,說明理由;
之間的關系是否仍然成立,說明理由;
(3)解決問題:如圖3,已知![]() ,連接
,連接![]() ,把線段AB繞點A旋轉,若
,把線段AB繞點A旋轉,若![]() ,請直接寫出線段
,請直接寫出線段![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
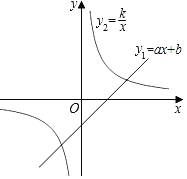
【題目】如圖,已知一次函數y1=ax+b(a≠0)與反比例函數y2=![]() (k>0),兩函數圖象交于(4,1),(﹣2,n)兩點.
(k>0),兩函數圖象交于(4,1),(﹣2,n)兩點.
(1)求a,k的值;
(2)若y2>y1>0,求x的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com