【題目】計算或解方程
（1）2
﹣3
+
（2）（﹣2）（+2）﹣（
）2
（3）（﹣3）0﹣
﹣|1﹣
|﹣
（4）3（3x﹣1）2﹣27＝0
（5）
＝﹣2
（6）x﹣2＝
【答案】（1）3
；（2）2
－6；（3）2－4；（4）x1＝
，x2＝－
；（5）x=－6；（6）x=
.
【解析】
（1）先化簡，再根據二次根式的加減法則計算即可；
（2）先利用完全平方公式、平方差公式計算，再進行實數混合運算計算即可；
（3）先去絕對值及化簡二次根式，再進行實數的混合運算即可；
（4）運用直接開方法解方程即可；
（5）利用立方根的定義求解即可；
（6）先解方程，再化簡即可.
解：（1）原式＝2﹣+2＝3；
（2）原式＝3﹣4﹣（2﹣2+3）
＝﹣1﹣5+2
＝2﹣6；
（3）原式＝1﹣3+1﹣
﹣（
）
＝1﹣3+1﹣﹣
＝2﹣4；
（4）（3x﹣1）2＝9，
3x﹣1＝±3，
解得x1＝，x2＝
；
（5）x﹣2＝﹣8，
x＝﹣6；
（6）x＝+2，
x＝
＝．
科目：初中數學 來源： 題型：
【題目】觀察表格,然后回答問題：
(1)表格中x= ;y= .
(2)從表格中探究a與
數位的規律,并利用這個規律解決下面兩個問題:
①已知
≈3.16,則
≈ ;
②已知
=8.973,若
=897.3,用含m的代數式表示b,則b= .
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知在ABCD中，AE⊥BC于點E，以點B為中心，取旋轉角等于∠ABC，把△BAE順時針旋轉得到△BA′E′，連接DA′，若∠ADC=60°，AD=5，DC=4，則DA′的大小為_____．
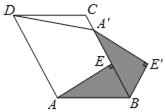
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】等邊三角形ABC的邊長為4 cm，點D從點C出發沿CA向點A運動，點E從點B出發沿AB的延長線BF向右運動，已知點D，E都以每秒
cm的速度同時開始運動，運動過程中DE與BC相交于點P.
(1).當點D，E運動多少秒后，△ADE為直角三角形?
(2)在點D，E運動時，線段PD與線段PE相等嗎?如果相等，予以證明;如不相等，說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在四邊形ABCD中，AB∥CD，∠ECF＝∠BCD＝90°，CE＝CF＝5，BC＝7，BD平分∠ABC，E是△BCD內一點，F是四邊形ABCD外一點．（E可以在△BCD的邊上）
（1）求證：DC＝BC；
（2）當∠BEC＝135°，設BE＝a，DE＝b，求a與b滿足的關系式；
（3）當E落在線段BD上時，求DE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，線段AB和射線BM交于點B．
（1）利用尺規完成以下作圖，并保留作圖痕跡（不寫做法）
①在射線BM上作一點C，使AC＝AB，連接AC
②作∠ABM的角平分線交AC于點D
③在射線CM上作一點E，使CE＝CD，連接DE
（2）在（1）中所作的圖形中，通過觀察和測量可以發現BD＝DE，請將下面的證明過程補充完整證明：∵AC＝AB，
∴∠ ＝∠
∵BD平分∠ABM，
∴∠DBE＝﹣
∠
∵CE＝CD
∴∠CDE＝∠CED
∴∠ACB＝∠CDE+∠CED，
∴∠CED＝∠ACB
∴∠DBE＝∠CED，
∴BD＝DE，（ ）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．
（1）請畫出△ABC關于y軸對稱的△A′B′C′（其中A′，B′，C′分別是A，B，C的對應點，不寫畫法）；
（2）直接寫出A′，B′，C′三點的坐標：A′（ ），B′（ ），C′（ ）
（3）計算△ABC的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲、乙兩家快遞公司攬件員（攬收快件的員工）的日工資方案如下：
甲公司為“基本工資+攬件提成”，其中基本工資為70元/日，每攬收一件提成2元；
乙公司無基本工資，僅以攬件提成計算工資．若當日攬件數不超過40，每件提成4元；若當日攪件數超過40，超過部分每件多提成2元．
如圖是今年四月份甲公司攬件員人均攬件數和乙公司攪件員人均攬件數的條形統計圖：
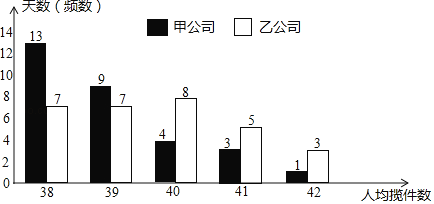
（1）現從今年四月份的30天中隨機抽取1天，求這一天甲公司攬件員人均攬件數超過40（不含40）的概率；
（2）根據以上信息，以今年四月份的數據為依據，并將各公司攬件員的人均攬件數視為該公司各攬件員的
攬件數，解決以下問題：
①估計甲公司各攬件員的日平均件數；
②小明擬到甲、乙兩家公司中的一家應聘攬件員，如果僅從工資收入的角度考慮，請利用所學的統計知識幫他選擇，井說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
