Question

【題目】閱讀下面材料：
數學課上，老師讓同學們解答課本中的習題：如圖1，在四邊形ABCD中，E、F、
G、H分別是各邊的中點，猜想四邊形EFGH的形狀并證明自己的猜想．
小麗在思考問題時，有如下思路：連接AC

結合小麗的思路作答：
（1）若只改變圖1中的四邊形ABCD的形狀（如圖2），則四邊形EFGH還是平行四邊形嗎？請說明理由

參考小麗思考問題方法，解決以下問題：
（2）如圖2，在（1）的條件下，若連接AC、BD
①當AC與BD滿足什么關系時，四邊形EFGH是菱形．寫出結論并證明．
②當AC與BD滿足什么關系時，四邊形EFGH是正方形．直接寫出結論

Answer 1

【答案】
（1）解：結論：四邊形EFGH還是平行四邊形．

理由：如圖2，連接AC．

∵E、F分別是AB、CB中點

∴EF∥AC，EF= AC，

同理：GH∥AC，GH= AC，

∴EF∥GH，EF=GH，

∴四邊形EFGH是平行四邊形

（2）解：①結論：當AC=BD時，四邊形EFGH是菱形．

理由：如圖3中，由（1）四邊形EFGH是平行四邊形

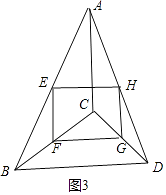
∵E、F是AB、CB中點

∴EF= AC

同理：EH= BD

∵AC=BD

∴EF=EH

∴平行四邊形EFGH是菱形．

②結論：當AC⊥BD且AC=BD時，四邊形EFGH是正方形．

理由：由①可知，AC=BD，四邊形EFGH是菱形，

∵AC⊥BD，AC∥HG，

∴HG⊥BD，

∵EH∥BD，

∴EH⊥HG，

∴∴∠EHG=90°，

∴四邊形EFGH是正方形

【解析】（1）結論：四邊形EFGH還是平行四邊形．只要證明EF=GH，EF∥GH即可；（2）①利用（1）的結論，只要證明EF=EH即可；②在①基礎上，只要證明∠EHG=90°即可；
【考點精析】掌握平行四邊形的性質是解答本題的根本，需要知道平行四邊形的對邊相等且平行；平行四邊形的對角相等，鄰角互補；平行四邊形的對角線互相平分．