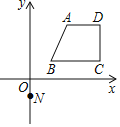
【題目】如圖，過點N（0，-1）的直線y=kx+b與圖中的四邊形ABCD有不少于兩個交點，其中A（2，3）、B（1，1）、C（4，1）、D（4，3），則k的取值范圍____________
永乾教育寒假作業快樂假期延邊人民出版社系列答案科目：初中數學 來源： 題型：
【題目】每年的
月
日為世界環保日，為了提倡低碳環保，某公司決定購買
臺節省能源的新設備，現有甲、乙兩種型號的設備可供選購.經調查：購買
臺甲型設備比購買
臺乙型設備多花
萬元，購買臺甲型設備比購買臺乙型設備少花萬元.
（1）求甲、乙兩種型號設備每臺的價格；
（2）該公司經決定購買甲型設備不少于臺，預算購買節省能源的新設備資金不超過
萬元，你認為該公司有哪幾種購買方案；
（3）在（2）的條件下，已知甲型設備每月的產量為
噸，乙型設備每月的產量為
噸.若每月要求產量不低于
噸，為了節約資金，請你為該公司設計一種最省錢的購買方案.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某中學七、八年級各選
名同學參加“創全國文明城市”知識競賽,計分分制,選手得分均為整數,成績達到
分或分以上為合格,達到
分或分以上為優秀,這次競賽后,七、八年級兩支代表隊成績分布的條形統計圖和成績分析表如下,其中七年級代表隊得分、分選手人數分別為
,
．
隊列 | 平均分 | 中位數 | 方差 | 合格率 | 優秀率 |
七年級 |
|
|
|
|
|
八年級 |
|
|
|
|
|
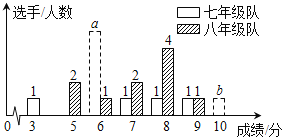
(1)根據圖表中的數據,求,
的值.
(2)直接寫出表中的
,
．
(3)你是八年級學生,請你給出兩條支持八年級隊成績好的理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
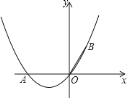
【題目】如圖，在直角坐標系中，點
的坐標為
，
，且
．
求經過，
，
三點的拋物線的解析式．
在中拋物線的對稱軸上是否存在點
，使
的周長最小？若存在，求出點的坐標；若不存在，請說明理由．
若點
為拋物線上一點，點
為對稱軸上一點，是否存在點，使得，，，構成的四邊形是平行四邊形？若存在，求出點的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲、乙兩名隊員參加射擊訓練，每人射擊10次，成績分別如下：
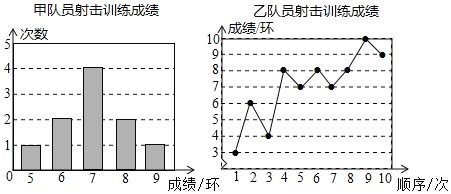
根據以上信息，整理分析數據如下：
平均成績/環 | 中位數/環 | 眾數/環 | 方差 | |
甲 |
| 7 | 7 | 1.2 |
乙 | 7 |
|
| 4.2 |
（1）
__________；
_____________；
__________；
（2）填空：（填“甲”或“乙”）
①從平均數和中位數的角度來比較，成績較好的是__________；
②從平均數和眾數的角度來比較，成績較好的是_________________；
③成績相對較穩定的是______________.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知拋物線
經過點E（1，0）和F（5，0），并交y軸于D（0，-5）；拋物線
：
（a≠0），
（1）試求拋物線的函數解析式；
（2）求證： 拋物線 與x軸一定有兩個不同的交點；
（3）若a=1
①拋物線、頂點分別為 （ ， ）、（ ， ） ；當x的取值范圍是_________ 時，拋物線、 上的點的縱坐標同時隨橫坐標增大而增大；
②已知直線MN分別與x軸、、分別交于點P（m，0）、M、N，且MN∥y軸，當1≤m≤5時，求線段MN的最大值。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知△ABC的面積為24，點D在線段AC上，點F在線段BC的延長線上，且BF＝4CF，四邊形DCFE是平行四邊形，則圖中陰影部分的面積為（ ）
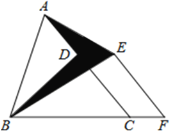
A.3B.4C.6D.8
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀與思考：
因式分解----“分組分解法”：分組分解法指通過分組分解的方式來分解用提公因式法和公式法無法直接分解的多項式，比如，四項的多項式一般按照“兩兩”分組或“三一”分組進行分組分解.分析多項式的特點，恰當的分組是分組分解法的關鍵.
例1：“兩兩”分組：
我們把
和
兩項分為一組，
和
兩項分為一組，分別提公因式，立即解除了困難.同樣.這道題也可以這樣做：
例2：“三一”分組：
我們把
，
，
三項分為一組，運用完全平方公式得到
，再與－1用平方差公式分解，問題迎刃而解.
歸納總結：用分組分解法分解因式的方法是先恰當分組，然后用提公因式法或運用公式法繼續分解.
請同學們在閱讀材料的啟發下，解答下列問題：
（1）分解因式：
①
；
②
（2）若多項式
利用分組分解法可分解為
，請寫出
，
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
