
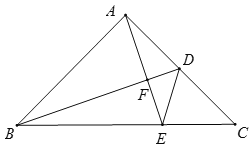
【題目】如圖,![]() 中,
中,![]() ,
,![]() ,
,![]() 是中線,
是中線,![]() ,垂足為
,垂足為![]() ,
,![]() 的延長線交
的延長線交![]() 于點(diǎn)
于點(diǎn)![]() ,若
,若![]() ,則
,則![]() 的度數(shù)為( )
的度數(shù)為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
作CH⊥AC,交AE延長線于H,先證明△ABD≌△CAH,得到∠ADB=∠H,再證明△CDE≌△CHE,得到∠CDE=∠H=∠ADB,再根據(jù)![]() 求出答案.
求出答案.
作CH⊥AC,交AE延長線于H,
∵![]() ,
,![]() ,
,
∴∠ABD+∠BAF=∠CAH+∠BAF=90![]() ,∠ACH=
,∠ACH=![]() ,
,
∴∠ABD=∠CAH,
∵AB=AC,
∴△ABD≌△CAH,
∴∠ADB=∠H,∠ACH=![]() ,AD=CH,
,AD=CH,
∵![]() ,AB=AC,
,AB=AC,
∴∠ACB=45![]() ,
,
∴∠ECH=∠ACB=∠ABC=45![]() ,
,
∵BD是中線,
∴CD=AD=CH,
∵CE=CE,
∴△CDE≌△CHE,
∴∠CDE=∠H=∠ADB,
∵![]() ,
,
∴∠ABD=25![]() ,
,
∴∠CDE=∠ADB=90![]() ∠ABD=
∠ABD=![]() ,
,
故選:D.



 提分百分百檢測卷單元期末測試卷系列答案
提分百分百檢測卷單元期末測試卷系列答案 小學(xué)期末標(biāo)準(zhǔn)試卷系列答案
小學(xué)期末標(biāo)準(zhǔn)試卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列函數(shù)中,y隨x增大而減小的有_____(填序號(hào)).
①y=![]() ;②y=x﹣2;③y=﹣3x+1;④y=
;②y=x﹣2;③y=﹣3x+1;④y=![]() ;⑤y=
;⑤y=![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
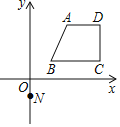
【題目】如圖,過點(diǎn)N(0,-1)的直線y=kx+b與圖中的四邊形ABCD有不少于兩個(gè)交點(diǎn),其中A(2,3)、B(1,1)、C(4,1)、D(4,3),則k的取值范圍____________
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在Rt△ABC中,∠C=90°,兩銳角的度數(shù)之比為2:1,其最短邊為1,射線CP交AB所在的直線于點(diǎn)P,且∠ACP=30°,則線段CP的長為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,一段拋物線:y=﹣x(x﹣2)(0≤x≤2)記為C1,它與x軸交于兩點(diǎn)O,A1;將C1繞A1旋轉(zhuǎn)180°得到C2,交x軸于A2;將C2繞A2旋轉(zhuǎn)180°得到C3,交x軸于A3;…如此進(jìn)行下去,直至得到C2018,若點(diǎn)P(4035,m)在第2018段拋物線C2018上,則m的值是

A. 1 B. -1 C. 0 D. 4035
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知直線l與⊙O相離,OA⊥l于點(diǎn)A,交⊙O于點(diǎn)P,點(diǎn)B是⊙O 上一點(diǎn),AB是⊙O的切線,連接BP并延長,交直線l于點(diǎn)C.
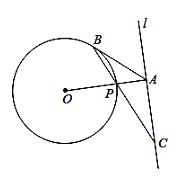
(1)求證AB=AC;
(2)若PC=![]() ,OA=15,求⊙O的半徑的長.
,OA=15,求⊙O的半徑的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系xOy中,點(diǎn)O為坐標(biāo)原點(diǎn),正方形OABC的邊OA,OC分別在x軸,y軸上,點(diǎn)B的坐標(biāo)為(4,4),反比例函數(shù)![]() 的圖象經(jīng)過線段BC的中點(diǎn)D,交正方形OABC的另一邊AB于點(diǎn)E.
的圖象經(jīng)過線段BC的中點(diǎn)D,交正方形OABC的另一邊AB于點(diǎn)E.
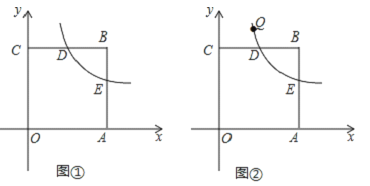
(1)求k的值;
(2)如圖①,若點(diǎn)P是x軸上的動(dòng)點(diǎn),連接PE,PD,DE,當(dāng)△DEP的周長最短時(shí),求點(diǎn)P的坐標(biāo);
(3)如圖②,若點(diǎn)Q(x,y)在該反比例函數(shù)圖象上運(yùn)動(dòng)(不與D重合),過點(diǎn)Q作QM⊥y軸,垂足為M,作QN⊥BC所在直線,垂足為N,記四邊形CMQN的面積為S,求S關(guān)于x的函數(shù)關(guān)系式,并寫出x的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
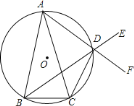
【題目】如圖,已知![]() 是
是![]() 的外接圓,
的外接圓,![]() ,
,![]() 是劣弧
是劣弧![]() 上的點(diǎn)(不與點(diǎn)
上的點(diǎn)(不與點(diǎn)![]() 、
、![]() 重合),延長
重合),延長![]() 至
至![]() .
.
![]() 求證:
求證:![]() 的延長線
的延長線![]() 平分
平分![]() ;
;
![]() 若
若![]() ,
,![]() 中
中![]() 邊上的高為
邊上的高為![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
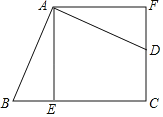
【題目】如圖,四邊形ABCD的∠BAD=∠C=90°,AB=AD,AE⊥BC于E,△ABE繞著點(diǎn)A旋轉(zhuǎn)后能與△ADF重合,若AF=5cm,則四邊形ABCD的面積為_____.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com