
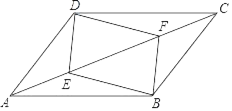
【題目】已知:如圖,E、F是ABCD的對角線AC上的兩點,AF=CE.
求證:(1)△ABE≌△CDF;
(2)ED∥BF.
【答案】(1)見解析;(2)見解析
【解析】
(1)根據已知條件得到AE=CF,根據平行四邊形的性質得到∠DCF=∠BAE,根據全等三角形的判定定理即可得到結論;
(2)根據全等三角形的性質得到BE=DF,∠AEB=∠CFD,根據平行四邊形的判定和性質即可得到結論.
證明:(1)∵AF=CE,
∴AF﹣EF=CE﹣EF,
即AE=CF,
∵四邊形ABCD是平行四邊形,
∴AB=CD,AB∥CD,
∴∠DCF=∠BAE,
在△ABE與△CDF中,
∵![]() ,
,
![]() ,
,
![]() ,
,
∴△ABE≌△CDF(SAS);
(2)∵△ABE≌△CDF,
∴BE=DF,∠AEB=∠CFD,
∴∠BEF=∠DFE,
∴BE∥DF,
∴四邊形DEBF是平行四邊形,
∴ED∥BF.


科目:初中數學 來源: 題型:
【題目】若一個四位自然數n滿足千位與個位相同,百位與十位相同,我們稱這個數為“天平數”.將“天平數”n的前兩位與后兩位交換位置得到一個新的“天平數”n′,記F(n)=![]() ,例如n=2112,n′=1221,F(2112)=
,例如n=2112,n′=1221,F(2112)=![]() =9
=9
(1)計算F(5335)= ;若“天平數”n滿足F(n)是一個完全平方數,求F(n)的值;
(2)s、t“天平數“,其中s=![]() ,t=
,t=![]() (1≤b<a≤9,1≤x<y≤9且a,b, xy為整數),若F(s)能被8整除,且F(s)+F(t)﹣9(y+1)=0,規定:K(s,t)=
(1≤b<a≤9,1≤x<y≤9且a,b, xy為整數),若F(s)能被8整除,且F(s)+F(t)﹣9(y+1)=0,規定:K(s,t)=![]() ,求K(s,t)的所有結果的值.
,求K(s,t)的所有結果的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
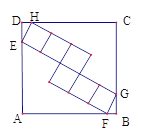
【題目】如圖,正方形ABCD中,內部有6個全等的正方形,小正方形的頂點E、F、G、H分別在邊AD、AB、BC、CD上,則tan∠DEH=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知等邊△ABC,點D在直線BC上,連接AD,作∠ADN=60°,直線DN交射線AB于點E,過點C作CF∥AB交直線DN于點F.
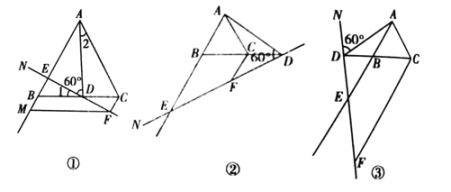
(1)當點D在線段BC上,∠NDB為銳角時,如圖①.
①判斷∠1與∠2的大小關系,并說明理由;
②過點F作FM∥BC交射線AB于點M,求證:CF+BE=CD;
(2)①當點D在線段BC的延長線上,∠NDB為銳角時,如圖②,請直接寫出線段CF,BE,CD之間的數量關系;
②當點D在線段CB的延長線上,∠NDB為鈍角或直角時,如圖③,請直接寫出線段CF,BE,CD之間的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:法國數學家韋達在研究一元二次方程時有一項重大發現:如果一元二次方程![]() 的兩個根分別是
的兩個根分別是![]() ,那么
,那么![]() ,
,![]() .
.
例如:已知方程![]() 的兩根分別是
的兩根分別是![]() ,
,
則:![]() ,
,![]() .
.
請同學們閱讀后利用以上結論完成以下問題:
(1)已知方程![]() 的兩根分別是
的兩根分別是![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)已知方程![]() 的兩根分別是
的兩根分別是![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)若一元二次方程![]() 的一個根大于2,一個根小于2,求
的一個根大于2,一個根小于2,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
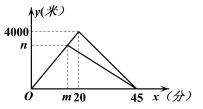
【題目】曉琳和爸爸到太子河公園運動,兩人同時從家出發,沿相同路線前行,途中爸爸有事返回,曉琳繼續前行5分鐘后也原路返回,兩人恰好同時到家.曉琳和爸爸在整個運動過程中離家的路程y1(米),y2(米)與運動時間x(分)之間的函數關系如圖所示,下列結論:①兩人同行過程中的速度為200米/分;②m的值是15,n的值是3000;③曉琳開始返回時與爸爸相距1800米;④運動18分鐘或30分鐘時,兩人相距900米.其中正確結論的個數是( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,兩個完全相同的三角形紙片![]() 和
和![]() 重合放置,其中
重合放置,其中![]() ,
,![]() .
.
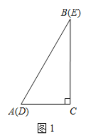

(1)操作發現:如圖2,固定![]() ,使
,使![]() 繞點
繞點![]() 旋轉,當點
旋轉,當點![]() 恰好落在
恰好落在![]() 邊上時,填空:①線段
邊上時,填空:①線段![]() 與
與![]() 的位置關系是________;②設
的位置關系是________;②設![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,則
,則![]() 與
與![]() 的數量關系是_____.
的數量關系是_____.
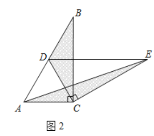
(2)猜想論證:當![]() 繞點
繞點![]() 旋轉到如圖3所示的位置時,請猜想(1)中
旋轉到如圖3所示的位置時,請猜想(1)中![]() 與
與![]() 的數量關系是否仍然成立?若成立,請證明;若不成立,請說明理由.
的數量關系是否仍然成立?若成立,請證明;若不成立,請說明理由.
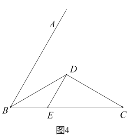
(3)拓展探究:已知![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于點
于點![]() (如圖4).若在射線
(如圖4).若在射線![]() 上存在點
上存在點![]() ,使
,使![]() ,請求相應的
,請求相應的![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com