
【題目】如圖1,點![]() 是線段
是線段![]() 的中點,分別以
的中點,分別以![]() 和
和![]() 為邊在線段
為邊在線段![]() 的同側作等邊三角形
的同側作等邊三角形![]() 和等邊三角形
和等邊三角形![]() ,連結
,連結![]() 和
和![]() ,相交于點
,相交于點![]() ,連結
,連結![]() ,
,
(1)求證:![]() ;
;
(2)求![]() 的大小;
的大小;
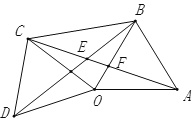
(3)如圖2,![]() 固定不動,保持
固定不動,保持![]() 的形狀和大小不變,將
的形狀和大小不變,將![]() 繞著點
繞著點![]() 旋轉(
旋轉(![]() 和
和![]() 不能重疊),求
不能重疊),求![]() 的大小.
的大小.
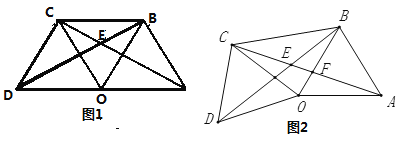
【答案】(1)證明見解析;(2)∠AEB=60°;(3)∠AEB=60°.
【解析】
(1)由等邊三角形的性質可得![]() ,
,![]() ,繼而可得∠AOC=∠DOB,利用SAS證明
,繼而可得∠AOC=∠DOB,利用SAS證明![]() ,利用全等三角形的性質即可得;;
,利用全等三角形的性質即可得;;
(2)先證明![]() ,從而可得 ∠ODB=∠DBO,再利用三角形外角的性質可求得
,從而可得 ∠ODB=∠DBO,再利用三角形外角的性質可求得![]() ,
,![]() ,進而根據
,進而根據![]() 即可求得答案;
即可求得答案;
(3)證明![]() ,從而可得
,從而可得![]() ,再由
,再由![]() ,可得
,可得![]() ,設
,設![]() 與
與![]() 交于點
交于點![]() ,利用三角形內角和定理以及對頂角的性質即可求得
,利用三角形內角和定理以及對頂角的性質即可求得![]() .
.
(1)∵![]() 和
和![]() 均為等邊三角形,
均為等邊三角形,
∴![]() ,
,![]() ,
,
∴![]()
![]() ,
,
即∠AOC=∠DOB,
∴![]() (SAS)
(SAS)
∴![]() ;
;
(2)∵O為AD中點,
∴DO=AO,
∵OA=OB,
∴![]() ,
,
∴∠ODB=∠DBO,
∵∠ODB+∠DBO=∠AOB=60°,
∴![]()
同理,![]() ,
,
∴![]() ;
;
(3)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵CO=DO,AO=BO,AO=DO,
∴OC=OB,
∴![]() (SAS),
(SAS),
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
設![]() 與
與![]() 交于點
交于點![]() ,
,
∵![]() ,
,![]() ,
,
又![]() ,
,
∴![]() .
.


科目:初中數學 來源: 題型:
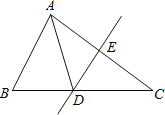
【題目】如圖,在△ABC中,AC的垂直平分線交BC于D,交AC于E,AE=3cm, △ABD的周長為13cm,那么△ABC的周長為_______________cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,AB=3cm,BC=5cm;,BE平分∠ABC,交AD于點E,交CD延長線于點F,則DE+DF的長度為_________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在Rt△ABC中,∠A=90°,AB=AC,點D,E分別在邊AB,AC上,AD=AE,連接DC,點M,P,N分別為DE,DC,BC的中點.
(1)觀察猜想
圖1中,線段PM與PN的數量關系是 ,位置關系是 ;
(2)探究證明
把△ADE繞點A逆時針方向旋轉到圖2的位置,連接MN,BD,CE,判斷△PMN的形狀,并說明理由;
(3)拓展延伸
把△ADE繞點A在平面內自由旋轉,若AD=4,AB=10,請直接寫出△PMN面積的最大值.

查看答案和解析>>
科目:初中數學 來源: 題型:
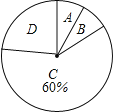
【題目】今年3月,某集團隨機抽取所屬的m家商業連鎖店進行評估,將各連鎖店按照評估成績分成了A、B、C、D四個等級,繪制了如圖尚不完整的統計圖表.
評估成績 | 評定等級 | 頻數 |
| A | 2 |
| B | b |
| C | 15 |
| D | 6 |
根據以上信息解答下列問題:
(1)求m,b的值;
(2)在扇形統計圖中,求B等級所在扇形的圓心角的大小;
(3)從評估成績不少于80分的連鎖店中,任選2家介紹營銷經驗,用樹狀圖或列表法求其中至少有一家是A等級的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點C是直線AB,DE之間的一點,∠ACD=90°,下列條件能使得AB∥DE的是( )
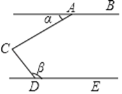
A. ∠α+∠β=180° B. ∠β﹣∠α=90° C. ∠β=3∠α D. ∠α+∠β=90°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),![]() ,
,![]() ,
,![]() 垂足分別為
垂足分別為![]() 、
、![]() ,
,![]() .點
.點![]() 在線段
在線段![]() 上以
上以![]() 的速度由點
的速度由點![]() 向點
向點![]() 運動,同時點
運動,同時點![]() 在射線
在射線![]() 上運動.它們運動的時間為
上運動.它們運動的時間為![]() (當點
(當點![]() 運動結束時,點
運動結束時,點![]() 運動隨之結束).
運動隨之結束).
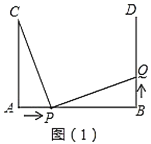
(1)若點![]() 的運動速度與點
的運動速度與點![]() 的運動速度相等,當
的運動速度相等,當![]() 時,
時,![]() 與
與![]() 是否全等,并判斷此時線段
是否全等,并判斷此時線段![]() 和線段
和線段![]() 的位置關系,請分別說明理由;
的位置關系,請分別說明理由;
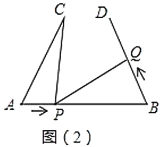
(2)如圖(2),若“![]() ,
,![]() ”改為“
”改為“![]() ”,點
”,點![]() 的運動速度為
的運動速度為![]() ,其它條件不變,當點
,其它條件不變,當點![]() 、
、![]() 運動到何處時有
運動到何處時有![]() 與
與![]() 全等,求出相應的
全等,求出相應的![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于二次函數y=ax2+bx+c的圖象有下列命題,其中是假命題的個數是( )
①當c=0時,函數的圖象經過原點;
②當b=0時,函數的圖象關于y軸對稱;
③函數的圖象最高點的縱坐標是![]() ;
;
④當c>0且函數的圖象開口向下時,方程ax2+bx+c=0必有兩個不相等的實根.
A. 0個 B. 1個 C. 2個 D. 3個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中點,E是AD的中點.過點A作AF∥BC交BE的延長線于點F.
,D是BC的中點,E是AD的中點.過點A作AF∥BC交BE的延長線于點F.

(1)求證:△AEF≌△DEB;
(2)證明四邊形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com