【題目】長沙市教育局組織部分教師分別到A、B、C、D四個地方進行課程培訓，教育局按定額購買了前往四地的車票，如圖1是未制作完成的車票種類和數量的條形統計圖，請根據統計圖回答下列問題：
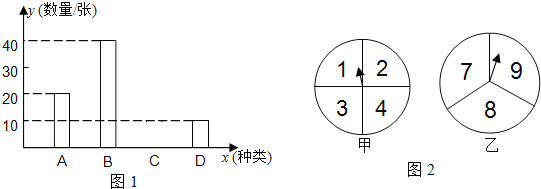
（1）若去A地的車票占全部車票的20%，求去C地的車票數，并補全條形統計圖（圖1）；
（2）請從小到大寫出這四類車票數的數字，并直接寫出這四個數據的平均數和中位數；
（3）如圖2，甲轉盤被分成四等份且標有數字1、2、3、4，乙轉盤分成三等份且標有數字7、8、9，具體規定是：同時轉動兩個轉盤，當指針指向的兩個數字之和是偶數時，李老師出去培訓，否則張老師出去培訓（指針指在線上重轉），試用“列表法”或“樹狀圖”的方法分析這個規定對雙方是否公平．
【答案】（1）30張，見解析；（2）10、20、30、40，平均數為25，中位數為25；（3）公平，見解析
【解析】
（1）先由去A地的車票占全部車票的20%求出車票總數，總數量減去A、B、D的數量即可求得C的數量，從而補全圖形；
（2）將四個數字從小到大排列，根據平均數和中位數的概念求解可得；
（3）根據題意用列表法分別求出當指針指向的兩個數字之和是偶數時的概率，即可求出這個規定對雙方是否公平．
解：（1）∵全部車票數為20÷20%＝100（張），
∴去C地車票數為100﹣（20+40+10）＝30（張），
補全圖形如下：
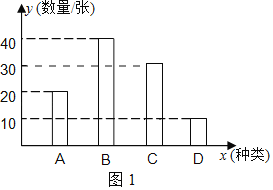
（2）從小到大寫出這四類車票數的數字為：10、20、30、40，
則這四個數據的平均數為
＝25，中位數為
＝25；
（3）根據題意列表如下：
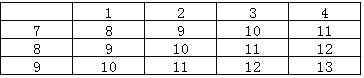
因為兩個數字之和是偶數時的概率是
＝
，
∴李老師出去培訓的概率和張老師出去培訓的概率相等，均為，
故這個規定對雙方是公平的．
暑假作業海燕出版社系列答案科目：初中數學 來源： 題型：
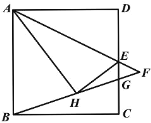
【題目】如圖，在正方形ABCD中，AB＝2，點E是CD的中點，連接AE，將△ADE沿AE折疊至△AHE，連接BH，延長AE，BH交于點F；BF，CD交于點G，則FG=_______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】國家為支持大學生創業，提供小額無息貸款，學生王芳享受政策無息貸款
元用來代理品牌服裝的銷售．已知該品牌服裝進價每件
元，日銷售
（件）與銷售價
（元/件）之間的關系如圖所示（實線），每天付員工的工資每人每天
元，每天應支付其它費用
元．
求日銷售（件）與銷售價（元/件）之間的函數關系式；
若暫不考慮還貸，當某天的銷售價為
元/件時，收支恰好平衡（收入
支出），求該店員工人數；
若該店只有
名員工，則該店至少需要多少天才能還清貸款，此時，每件服裝的價格應定為多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】中華文明，源遠流長，中華漢字，寓意深廣.為傳承中華優秀傳統文化，某中學德育處組織了一次全校2000名學生參加的“漢字聽寫”大賽.為了解本次大賽的成績，學校德育處隨機抽取了其中200名學生的成績作為樣本進行統計，制成如下不完整的統計圖表：
成績x（分）分數段 | 頻數（人） | 頻率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | 0.2 |
80≤x<90 | m | 0.35 |
90≤x<100 | 50 | n |
頻數分布直方圖
根據所給的信息，回答下列問題：
（1）m=________；n=________；
（2）補全頻數分布直方圖；
（3）這200名學生成績的中位數會落在________分數段；
（4）若成績在90分以上（包括90分）為“優”等，請你估計該校參加本次比賽的2000名學生中成績是“優”等的約有多少人？
查看答案和解析>>
科目：初中數學 來源： 題型：
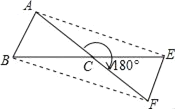
【題目】將△ABC繞點C旋轉180°得到△FEC．
（1）試猜想AE與BF有何關系？說明理由．
（2）若△ABC的面積為3cm2，求四邊形ABFE的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】定義：在線段MN上存在點P、Q將線段MN分為相等的三部分，則稱P、Q為線段MN的三等分點．
已知一次函數y＝﹣x+3的圖象與x、y軸分別交于點M、N，且A、C為線段MN的三等分點（點A在點C的左邊）．
（1）直接寫出點A、C的坐標；
（2）①二次函數的圖象恰好經過點O、A、C，試求此二次函數的解析式；
②過點A、C分別作AB、CD垂直x軸于B、D兩點，在此拋物線O、C之間取一點P（點P不與O、C重合）作PF⊥x軸于點F，PF交OC于點E，是否存在點P使得AP＝BE？若存在，求出點P的坐標？若不存在，試說明理由；
（3）在（2）的條件下，將△OAB沿AC方向移動到△O'A'B'（點A'在線段AC上，且不與C重合），△O'A'B'與△OCD重疊部分的面積為S，試求當S＝
時點A'的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB是⊙O的直徑， BC交⊙O于點D，E是
的中點，連接AE交BC于點F，∠ACB =2∠EAB．
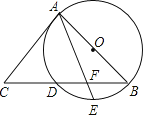
（1）求證：AC是⊙O的切線；
（2）若
，
，求BF的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）證明推斷：如圖（1），在正方形ABCD中，點E，Q分別在邊BC，AB上，DQ⊥AE于點O，點G，F分別在邊CD，AB上，GF⊥AE．
①求證：DQ＝AE；
②推斷：
的值為 ；
（2）類比探究：如圖（2），在矩形ABCD中，
＝k（k為常數）．將矩形ABCD沿GF折疊，使點A落在BC邊上的點E處，得到四邊形FEPG，EP交CD于點H，連接AE交GF于點O．試探究GF與AE之間的數量關系，并說明理由；
（3）拓展應用：在（2）的條件下，連接CP，當k＝
時，若tan∠CGP＝
，GF＝2
，求CP的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
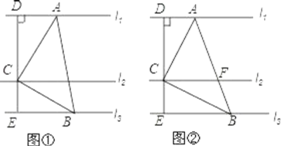
【題目】探究：如圖①，直線l1∥l2∥l3，點C在l2上，以點C為直角頂點作∠ACB＝90°，角的兩邊分別交l1與l3于點A、B，連結AB，過點C作CD⊥l1于點D，延長DC交l3于點E．
（1）求證：△ACD∽△CBE．
（2）應用：如圖②，在圖①的基礎上，設AB與l2的交點為F，若AC＝BC，l1與l2之間的距離為2，l2與l3之間的距離為1，則AF的長度是 ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com