
【題目】平面直角坐標中,已知點O(0,0),A(0,2),B(1,0),點P是反比例函數(shù)y=- ![]()
圖象上的一個動點,過點P作PQ⊥x軸,垂足為Q . 若以點O、P、Q為頂點的三角形與△OAB相似,則相應的點P共有( ).
A.1個
B.2個
C.3個
D.4個
【答案】D
【解析】∵點P是反比例函數(shù)y=- ![]() 圖象上,
圖象上,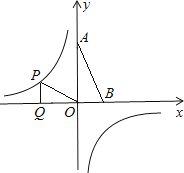
∴設點P(x , y),
當△PQO∽△AOB時,則 ![]() =
= ![]() ,
,
又PQ=y , OQ=-x , OA=2,OB=1,
即 ![]() =
= ![]() ,即y=-2x ,
,即y=-2x ,
∵xy=-1,即-2x2=-1,
∴x=± ![]() ,
,
∴點P為( ![]() ,-
,- ![]() )或(-
)或(- ![]() ,
, ![]() );
);
同理,當△PQO∽△BOA時,
求得P(- ![]() ,
, ![]() )或(
)或( ![]() ,-
,- ![]() );
);
故相應的點P共有4個.
故選:D .
可以分別從△PQO∽△AOB與△PQO∽△BOA去分析,首先設點P(x , y),根據(jù)相似三角形的對應邊成比例與反比例函數(shù)的解析式,聯(lián)立可得方程組,解方程組即可求得點P的坐標,即可求得答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,CD⊥AB , 垂足為D , AB=c , ∠a=α , 則CD長為( ) 
A.csin2α
B.ccos2α
C.csinαtanα
D.csinαcosα
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】問題背景:在△ABC中,AB、BC、AC三邊的長分別為![]() 、
、![]() 、
、![]() ,求此三角形的面積.小輝同學在解答這道題時,先建立一個正方形網(wǎng)格(每個小正方形的邊長為1),再在網(wǎng)格中畫出格點△ABC(即△ABC三個頂點都在小正方形的頂點處),如圖①所示.這樣不需求△ABC的高,而借用網(wǎng)格就能計算出它的面積.
,求此三角形的面積.小輝同學在解答這道題時,先建立一個正方形網(wǎng)格(每個小正方形的邊長為1),再在網(wǎng)格中畫出格點△ABC(即△ABC三個頂點都在小正方形的頂點處),如圖①所示.這樣不需求△ABC的高,而借用網(wǎng)格就能計算出它的面積.
(1)請你將△ABC的面積直接填寫在橫線上: .
思維拓展:
(2)我們把上述求△ABC面積的方法叫做構圖法.如果△ABC三邊的長分別![]() a、
a、![]() a、
a、![]() a(a>0),請利用圖②的正方形網(wǎng)格(每個小正方形的邊長為a)畫出相應的△ABC,并求出它的面積.
a(a>0),請利用圖②的正方形網(wǎng)格(每個小正方形的邊長為a)畫出相應的△ABC,并求出它的面積.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在梯形ABCD中,AD∥BC , E、F分別是AB、CD的中點,則下列結(jié)論:
①EF∥AD;②S△ABO=S△DCO;③△OGH是等腰三角形;④BG=DG;⑤EG=HF .
其中正確的個數(shù)是( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在△ABC中,AB=6cm , AC=12cm , 動點M從點A出發(fā),以1cm∕秒的速度向點B運動,動點N從點C出發(fā),以2cm∕秒的速度向點A運動,若兩點同時運動,是否存在某一時刻t , 使得以點A、M、N為頂點的三角形與△ABC相似,若存在,求出t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,已知BD為△ABC的角平分線,請按如下要求操作解答:
(1)過點D畫DE∥BC交AB于E,若∠A=68°,∠AED=42°,求∠BDC的度數(shù).
(2)畫△ABC的角平分線CF交BD于點M,若∠A=60°,求∠CMD的度數(shù).

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系中,A(﹣2,2),B(﹣3,﹣2)
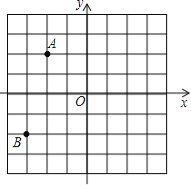
(1)若點C與點A關于原點O對稱,則點C的坐標為 ;
(2)將點A向右平移5個單位得到點D,則點D的坐標為 ;
(3)由點A,B,C,D組成的四邊形ABCD內(nèi)(不包括邊界)任取一個橫、縱坐標均為整數(shù)的點,求所取的點橫、縱坐標之和恰好為零的概率.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com