
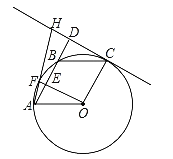
【題目】如圖,A、F、B、C是半圓O上的四個點,四邊形OABC是平行四邊形,∠FAB=15°,連接OF交AB于點E,過點C作OF的平行線交AB的延長線于點D,延長AF交直線CD于點H.
(1)求證:CD是半圓O的切線;
(2)若DH=![]() ,求EF和半徑OA的長.
,求EF和半徑OA的長.
【答案】(1)證明見解析;(2)EF=![]() ,r=2.
,r=2.
【解析】
試題分析:(1)連接OB,根據已知條件得到△AOB是等邊三角形,得到∠AOB=60°,根據圓周角定理得到∠AOF=∠BOF=30°,根據平行線的性質得到OC⊥CD,由切線的判定定理即可得到結論;
(2)根據平行線的性質得到∠DBC=∠EAO=60°,解直角三角形得到BD=![]() BC=
BC=![]() AB,推出AE=
AB,推出AE=![]() AD,根據相似三角形的性質得到
AD,根據相似三角形的性質得到![]() ,求得EF=
,求得EF=![]() ,根據直角三角形的性質即可得到結論.
,根據直角三角形的性質即可得到結論.
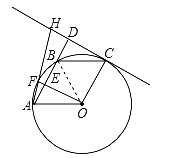
試題解析:(1)連接OB,∵OA=OB=OC,∵四邊形OABC是平行四邊形,∴AB=OC,∴△AOB是等邊三角形,∴∠AOB=60°,∵∠FAD=15°,∴∠BOF=30°,∴∠AOF=∠BOF=30°,∴OF⊥AB,∵CD∥OF,∴CD⊥AD,∵AD∥OC,∴OC⊥CD,∴CD是半圓O的切線;
(2)∵BC∥OA,∴∠DBC=∠EAO=60°,∴BD=![]() BC=
BC=![]() AB,∴AE=
AB,∴AE=![]() AD,∵EF∥DH,∴△AEF∽△ADH,∴
AD,∵EF∥DH,∴△AEF∽△ADH,∴![]() ,∵DH=
,∵DH=![]() ,∴EF=
,∴EF=![]() ,∵OF=OA,∴OE=OA﹣(
,∵OF=OA,∴OE=OA﹣(![]() ),∵∠AOE=30°,∴
),∵∠AOE=30°,∴![]() =
=![]() ,解得:OA=2.
,解得:OA=2.


 53隨堂測系列答案
53隨堂測系列答案科目:初中數學 來源: 題型:
【題目】某藥品研究所開發一種抗菌新藥,經多年動物實驗,首次用于臨床人體試驗,測得成人服藥后血液中藥物濃度y(微克/毫升)與服藥時間x小時之間函數關系如圖所示(當4≤x≤10時,y與x成反比例).
(1)根據圖象分別求出血液中藥物濃度上升和下降階段y與x之間的函數關系式.
(2)問血液中藥物濃度不低于4微克/毫升的持續時間多少小時?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某次數學趣味競賽共有10道題目,每道題答對得10分,答錯或不答得0分,全班40名同學參加了此次競賽,他們的得分情況如下表所示
成績(分) | 50 | 60 | 70 | 80 | 90 | 100 |
人數 | 2 | 5 | 13 | 10 | 7 | 3 |
則全班40名同學的成績的中位數和眾數分別是 。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,一次函數y=﹣ax+b的圖象與反比例函數![]() 的圖象相交于點A(﹣4,﹣2),B(m,4),與y軸相交于點C.
的圖象相交于點A(﹣4,﹣2),B(m,4),與y軸相交于點C.
(1)求反比例函數和一次函數的表達式;
(2)求點C的坐標及△AOB的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
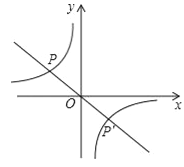
【題目】如圖,點P(﹣3,1)是反比例函數![]() 的圖象上的一點.
的圖象上的一點.
(1)求該反比例函數的解析式;
(2)設直線y=kx與雙曲線![]() 的兩個交點分別為P和P′,當
的兩個交點分別為P和P′,當![]() <kx時,直接寫出x的取值范圍.
<kx時,直接寫出x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠B、∠C的平分線相交于F,過點F作DE∥BC,交AB于D,交AC于E,那么下列結論:①△BDF、△CEF都是等腰三角形; ②DE=BD+CE;③△ADE的周長為AB+AC;④BD=CE.其中正確的是( ) 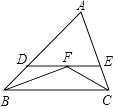
A.③④
B.①②
C.①②③
D.②③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com