
【題目】如圖,平面直角坐標系中,點A在第四象限,點B在x軸正半軸上,在△OAB中,∠OAB=90°,AB=AO=6![]() ,點P為線段OA上一動點(點P不與點A和點O重合),過點P作OA的垂線交x軸于點C,以點C為正方形的一個頂點作正方形CDEF,使得點D在線段CB上,點E在線段AB上.
,點P為線段OA上一動點(點P不與點A和點O重合),過點P作OA的垂線交x軸于點C,以點C為正方形的一個頂點作正方形CDEF,使得點D在線段CB上,點E在線段AB上.
(1)①求直線AB的函數表達式.
②直接寫出直線AO的函數表達式 ;
(2)連接PF,在Rt△CPF中,∠CFP=90°時,請直接寫出點P的坐標為 ;
(3)在(2)的前提下,直線DP交y軸于點H,交CF于點K,在直線OA上存在點Q.使得△OHQ的面積與△PKE的面積相等,請直接寫出點Q的坐標 .
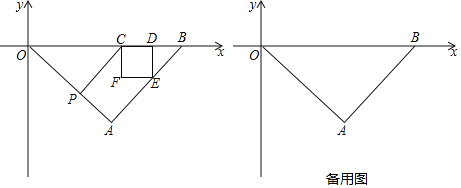
【答案】(1)①y=x﹣12;②y=﹣x;(2)(3,﹣3);(3)(2,﹣2)或(﹣2,2)
【解析】
(1)①利用等腰直角三角形的性質可以得到點A和點B的坐標,從而根據待定系數法求得直線AB的函數表達式;
②根據點A和點O的坐標可以求得直線AO的表達式;
(2)根據題意畫出圖形,首先得出點P、F、E三點共線,然后根據正方形的性質得出PE是△OAB的中位線,即點P為OA的中點,則點P的坐標可求;
(3)根據題意畫出圖形,然后求出直線PD 的解析式,得到點H的坐標,根據(2)中的條件和題意,可以求得△PKE的面積,再根據△OHQ的面積與△PKE的面積相等,可以得到點Q橫坐標的絕對值,由點Q在直線AO上即可求得點Q的坐標.
解:(1)①∵在△OAB中,∠OAB=90°,AB=AO=![]() ,
,
∴△AOB是等腰直角三角形,OB=![]() ,
,
∴∠AOB=∠ABO=45°,
∴點A的坐標為(6,﹣6),點B的坐標為(12,0),
設直線AB的函數表達式為y=kx+b,
![]() ,得
,得![]() ,
,
即直線AB的函數表達式是y=x﹣12;
②設直線AO的函數表達式為y=ax,
6a=﹣6,得a=﹣1,
即直線AO的函數表達式為y=﹣x,
(2)點P的坐標為(3,﹣3),
理由:如圖:

∵在Rt△CPF中,∠CFP=90°,∠CFE=90°,
∴點P、F、E三點共線,
∴PE∥OB,
∵四邊形CDEF是正方形,∠OPC=90°,∠COA=45°,
∴CF=PF=AF=EF,
∴PE是△OAB的中位線,
∴點P為OA的中點,
∴點P的坐標為(3,﹣3),
故答案為:(3,﹣3);
(3)如圖,
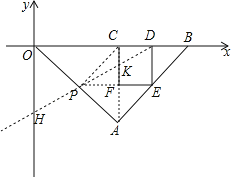
在△PFK和△DCK中,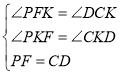
∴△PFK≌△DCK(AAS),
∴CK=FK,
則由(2)可知,PE=6,FK=1.5,BD=3
∴點D(9,0)
∴△PKE的面積是![]() =4.5,
=4.5,
∵△OHQ的面積與△PKE的面積相等,
∴△OHQ的面積是4.5,
設直線PD的函數解析式為y=mx+n
∵點P(3,﹣3),點D(9,0)在直線PD上,
∴![]() ,得
,得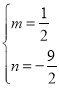 ,
,
∴直線PD的函數解析式為y=![]() ,
,
當x=0時,y=-![]() ,
,
即點H的坐標為![]() ,
,
∴OH=![]()
設點Q的橫坐標為q,
則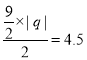 ,
,
解得,q=±2,
∵點Q在直線OA上,直線OA的表達式為y=﹣x,
∴當x=2時,y=﹣2,當x=﹣2時,x=2,
即點Q的坐標為(2,﹣2)或(﹣2,2),


科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是線段
是線段![]() 上一動點(
上一動點(![]() 不與
不與![]() ,
,![]() 重合).
重合).
(1)如圖1,當點![]() 為
為![]() 的中點,過點
的中點,過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,求證:
,求證:![]() ;
;
(2)連接![]() ,作
,作![]() ,
,![]() 交
交![]() 于點
于點![]() .若
.若![]() 時,如圖2.
時,如圖2.
①![]() ______;
______;
②求證:![]() 為等腰三角形;
為等腰三角形;
(3)連接CD,∠CDE=30°,在點![]() 的運動過程中,
的運動過程中,![]() 的形狀可以是等腰三角形嗎?若可以,請求出
的形狀可以是等腰三角形嗎?若可以,請求出![]() 的度數;若不可以,請說明理由.
的度數;若不可以,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將△ABC繞點C順時針旋轉90°得到△EDC.若點A,D,E在同一條直線上,∠ACB=20°,則∠ADC的度數是( )

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】跳遠運動員李陽對訓練效果進行測試.6次跳遠的成績如下:7.5,7.7,7.6,7.7,7.9,7.8(單位:m)這六次成績的平均數為7.7m,方差為![]() .如果李陽再跳一次,成績為7.7m.則李陽這7次跳遠成績的方差_____(填“變大”、“不變”或“變小”).
.如果李陽再跳一次,成績為7.7m.則李陽這7次跳遠成績的方差_____(填“變大”、“不變”或“變小”).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是等邊三角形,△ACE是等腰三角形,∠AEC=120°,AE=CE,F為BC中點,連接AE.
(1)直接寫出∠BAE的度數為 ;
(2)判斷AF與CE的位置關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為支援雅安災區,某學校計劃用“義捐義賣”活動中籌集的部分資金用于購買A,B兩種型號的學習用品共1000件,已知A型學習用品的單價為20元,B型學習用品的單價為30元.
(1)若購買這批學習用品用了26000元,則購買A,B兩種學習用品各多少件?
(2)若購買這批學習用品的錢不超過28000元,則最多購買B型學習用品多少件?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面的文字,解答問題:
![]() 是一個無理數,而無理數是無限不循環小數,因此
是一個無理數,而無理數是無限不循環小數,因此![]() 的小數部分無法全部寫出來,但是我們可以想辦法把它表示出來.因為
的小數部分無法全部寫出來,但是我們可以想辦法把它表示出來.因為![]() ,所以
,所以![]() 的整數部分為
的整數部分為![]() ,將
,將![]() 減去其整數部分后,得到的差就是小數部分,于是
減去其整數部分后,得到的差就是小數部分,于是![]() 的小數部分為
的小數部分為![]() .
.
(1)求出![]() 的整數部分和小數部分:
的整數部分和小數部分:
(2)求出![]() 的整數部分和小數部分;
的整數部分和小數部分;
(3)如果![]() 的整數部分是
的整數部分是![]() ,小數部分是
,小數部分是![]() ,求出
,求出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖![]() ,已知直線
,已知直線![]() 與
與![]() 軸,
軸,![]() 軸分別交于
軸分別交于![]() ,
,![]() 兩點,以
兩點,以![]() 為直角頂點在第二象限作等腰
為直角頂點在第二象限作等腰![]() .
.
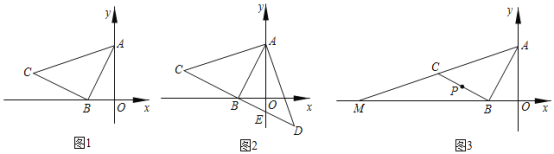
(1)求點![]() 的坐標,并求出直線
的坐標,并求出直線![]() 的關系式;
的關系式;
(2)如圖![]() ,直線
,直線![]() 交
交![]() 軸于
軸于![]() ,在直線
,在直線![]() 上取一點
上取一點![]() ,連接
,連接![]() ,若
,若![]() ,求證:
,求證:![]() .
.
(3)如圖![]() ,在(1)的條件下,直線
,在(1)的條件下,直線![]() 交
交![]() 軸于點
軸于點![]() ,
,![]() 是線段
是線段![]() 上一點,在
上一點,在![]() 軸上是否存在一點
軸上是否存在一點![]() ,使
,使![]() 面積等于
面積等于![]() 面積的一半?若存在,請求出點
面積的一半?若存在,請求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
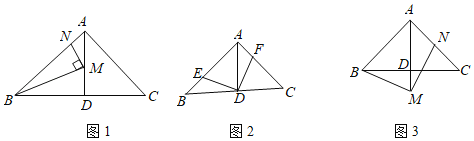
【題目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 于點
于點![]() .
.
(1)如圖1,點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 上,且
上,且![]() ,當
,當![]() ,
,![]() 時,求線段
時,求線段![]() 的長;
的長;
(2)如圖2,點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 上,且
上,且![]() ,求證:
,求證:![]() ;
;
(3)如圖3,點![]() 在
在![]() 的延長線上,點
的延長線上,點![]() 在
在![]() 上,且
上,且![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com