【題目】把幾個圖形拼成一個新的圖形，再通過圖形面積的計算，常常可以得到一些有用的式子，或可以求出一些不規則圖形的面積．
（1）如圖1，是將幾個面積不等的小正方形與小長方形拼成一個邊長為a+b+c的正方形，試用不同的方法計算這個圖形的面積，你能發現什么結論，請寫出來．
（2）如圖2，是將兩個邊長分別為a和b的正方形拼在一起，B、C、G三點在同一直線上，連接BD和BF，若兩正方形的邊長滿足a+b=10，ab=20，你能求出陰影部分的面積嗎？
【答案】（1）a2+b2+c2+2ab+2bc+2ac；（2）20
【解析】
試題分析:（1）此題根據面積的不同求解方法，可得到不同的表示方法．一種可以是3個正方形的面積和6個矩形的面積，種是大正方形的面積，可得等式
（a+b+c）2=a2+b2+c2+2ab+2bc+2ac，
（2）利用S陰影=正方形ABCD的面積+正方形ECGF的面積﹣三角形BGF的面積﹣三角形ABD的面積求解．
解（1）（a+b+c）2=a2+b2+c2+2ab+2bc+2ac
（2）∵a+b=10，ab=20，
∴S陰影=a2+b2﹣
（a+b）×b﹣a2=a2+b2﹣ab=（a+b）2﹣
ab=×102﹣×20=50﹣30=20．
科目：初中數學 來源： 題型：
【題目】建立模型：
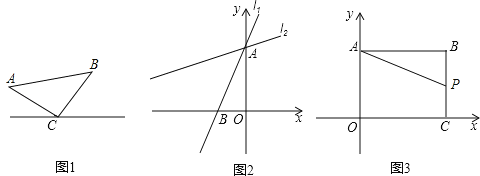
如圖1，已知△ABC，AC=BC，∠C=90°，頂點C在直線l上．
操作：
過點A作AD⊥l于點D，過點B作BE⊥l于點E．求證：△CAD≌△BCE．
模型應用：
（1）如圖2，在直角坐標系中，直線l1：y=
x+4與y軸交于點A，與x軸交于點B，將直線l1繞著點A順時針旋轉45°得到l2．求l2的函數表達式．
（2）如圖3，在直角坐標系中，點B（8，6），作BA⊥y軸于點A，作BC⊥x軸于點C，P是線段BC上的一個動點，點Q（a，2a﹣6）位于第一象限內．問點A、P、Q能否構成以點Q為直角頂點的等腰直角三角形，若能，請求出此時a的值，若不能，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】數學課上，李老師出示了如下框中的題目．
小敏與同桌小聰討論后，進行了如下解答：
（1）特殊情況探索結論
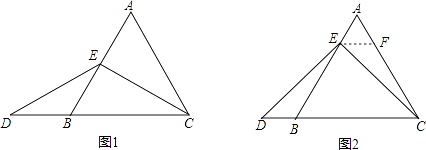
當點E為AB的中點時，如圖1，確定線段AE與的DB大小關系．請你直接寫出結論：AEDB（填“＞”，“＜”或“=”）．
（2）特例啟發，解答題目
解：題目中，AE與DB的大小關系是：AEDB（填“＞”，“＜”或“=”）．理由如下：
如圖2，過點E作EF∥BC，交AC于點F，（請你完成以下解答過程）
（3）拓展結論，設計新題
在等邊三角形ABC中，點E在直線AB上，點D在直線BC上，且ED=EC．若△ABC的邊長為1，AE=2，求CD的長（請你直接寫出結果）．
查看答案和解析>>
科目：初中數學 來源： 題型：
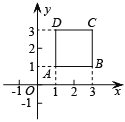
【題目】如圖所示，正方形ABCD的頂點坐標分別為A(1，1)，B(3，1)，C(3，3)，D(1，3).
(1)在同一直角坐標系中，將正方形向左平移2個單位，畫出相應的圖形，并寫出各點的坐標.
(2)將正方形向下平移2個單位，畫出相應的圖形，并寫出各點的坐標.
(3)在(1)(2)中，你發現各點的橫、縱坐標發生了哪些變化？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某市積極開展“陽光體育進校園”活動，各校學生堅持每天鍛煉一小時，某校根據實際，決定主要開設A：乒乓球，B：籃球，C：跑步，D：跳繩四種運動項目，為了解學生最喜歡哪一種項目，隨機抽取了部分學生進行調查，并將調查結果繪制成如下統計圖．請你結合圖中信息解答下列問題．
（1）請計算最喜歡B項目的人數所占的百分比．
（2）請計算D項所在扇形圖中的圓心角的度數．
（3）請把統計圖補充完整．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在ABCD中，AM，CN分別是∠BAD和∠BCD的平分線，添加一個條件，仍無法判斷四邊形AMCN為菱形的是（ ）
A．AM=AN B．MN⊥AC
C．MN是∠AMC的平分線 D．∠BAD=120°
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某汽車行駛時油箱中余油量Q（L）與行駛時間t（h）的關系如表：
行駛時間t/h | 余油量Q/L |
1 | 42 |
2 | 34 |
3 | 26 |
4 | 18 |
5 | 10 |
（1）汽車行駛之前油箱中有汽油多少升？
（2）用行駛時間t的代數式表示余油量Q（直接寫出答案）；
（3）當t＝
時，求余油量Q的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
