
【題目】某公司經營甲、乙兩種商品,兩種商品的進價和售價情況如下表:
進價(萬元/件) | 售價(萬元/件) | |
甲 | 12 | 14.5 |
乙 | 8 | 10 |
兩種商品的進價和售價始終保持不變.現準備購進甲、乙兩種商品共20件.設購進甲種商品![]() 件,兩種商品全部售出可獲得利潤為
件,兩種商品全部售出可獲得利潤為![]() 萬元.
萬元.
(1)![]() 與
與![]() 的函數關系式為__________________;
的函數關系式為__________________;
(2)若購進兩種商品所用的資金不多于200萬元,則該公司最多購進多少合甲種商品?
(3)在(2)的條件下,請你幫該公司設計一種進貨方案,使得該公司獲得最大利潤,并求出最大利潤是多少?
【答案】(1)w=0.5x+40;(2)10;(3)該公司購進甲種商品10件,乙種商品10件時,該公司獲得最大利潤,最大利潤是45萬元
【解析】
(1)設該公司購進甲種商品x件,則乙種商品(20﹣x)件,根據題意可得等量關系:公司獲得的利潤w=甲種商品的利潤+乙種商品的利潤,根據等量關系可得函數關系式;
(2)根據資金不多于20萬元列出不等式組;
(3)根據一次函數的性質:k>0時,w隨x的增大而增大可得答案.
解:(1)設該公司購進甲種商品x件,則乙種商品(20﹣x)件,
根據題意得:w=(14.5﹣12)x+(10﹣8)(20﹣x),
整理得:w=0.5x+40;
故答案為:w=0.5x+40;
(2)由題意得:12x+8(20﹣x)≤200,解得x≤10,
故該公司最多購進10臺甲種商品;
(3)∵對于函數w=0.5x+40,w隨x的增大而增大,
∴當x=10時,能獲得最大利潤,最大利潤為:w=0.5×10+40=45(萬元),
故該公司購進甲種商品10件,乙種商品10件時,該公司獲得最大利潤,最大利潤是45萬元.


科目:初中數學 來源: 題型:
【題目】問題探究:小明根據學習函數的經驗,對函數![]() 的圖象與性質進行了探究.
的圖象與性質進行了探究.
下面是小明的探究過程,請你解決相關問題:
![]() 在函數
在函數![]() 中,自變量x可以是任意實數;
中,自變量x可以是任意實數;
![]() 如表y與x的幾組對應值:
如表y與x的幾組對應值:
X |
|
|
|
|
| 0 | 1 | 2 | 3 | 4 |
|
Y |
|
| 0 | 1 | 2 | 3 | 2 | 1 | a |
|
|
![]() ______;
______;
![]() 若
若![]() ,
,![]() 為該函數圖象上不同的兩點,則
為該函數圖象上不同的兩點,則![]() ______;
______;
![]() 如圖,在平面直角坐標系中,描出以上表中各對對應值為坐標的點,并根據描出的點,畫出該函數的圖象:
如圖,在平面直角坐標系中,描出以上表中各對對應值為坐標的點,并根據描出的點,畫出該函數的圖象:
![]() 該函數有______
該函數有______![]() 填“最大值”或“最小值”
填“最大值”或“最小值”![]() ;并寫出這個值為______;
;并寫出這個值為______;
![]() 求出函數圖象與坐標軸在第二象限內所圍成的圖形的面積;
求出函數圖象與坐標軸在第二象限內所圍成的圖形的面積;
![]() 觀察函數
觀察函數![]() 的圖象,寫出該圖象的兩條性質.
的圖象,寫出該圖象的兩條性質.
查看答案和解析>>
科目:初中數學 來源: 題型:
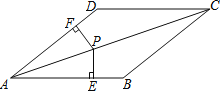
【題目】在四邊形ABCD中,AB//CD,∠B=∠D.
(1)求證:四邊形ABCD為平行四邊形;
(2)若點P為對角線AC上的一點,PE⊥AB于E,PF⊥AD于F,且PE=PF,求證:四邊形ABCD是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P是平行四邊形ABCD對角線BD上的動點,點M為AD的中點,已知AD=8,AB=10,∠ABD=45°,把平行四邊形ABCD繞著點A按逆時針方向旋轉,點P的對應點是點Q,則線段MQ的長度的最大值與最小值的差為__.
查看答案和解析>>
科目:初中數學 來源: 題型:
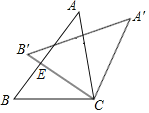
【題目】如圖1,在△ACB和△AED中,AC=BC,AE=DE,∠ACB=∠AED=90°,點E在AB上,F是線段BD的中點,連接CE、FE.
(1)若AD=3![]() ,BE=4,求EF的長;
,BE=4,求EF的長;
(2)求證:CE=![]() EF;
EF;
(3)將圖1中的△AED繞點A順時針旋轉,使AED的一邊AE恰好與△ACB的邊AC在同一條直線上(如圖2),連接BD,取BD的中點F,問(2)中的結論是否仍然成立,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,正方形![]() 中,點
中,點![]() 、
、![]() 的坐標分別為
的坐標分別為![]() ,
,![]() ,點
,點![]() 在第一象限.動點
在第一象限.動點![]() 在正方形
在正方形![]() 的邊上,從點
的邊上,從點![]() 出發沿
出發沿![]() 勻速運動,同時動點
勻速運動,同時動點![]() 以相同速度在
以相同速度在![]() 軸上運動,當點
軸上運動,當點![]() 運動到點
運動到點![]() 時,兩點同時停止運動,設運動時間為
時,兩點同時停止運動,設運動時間為![]() 秒.當點
秒.當點![]() 在邊
在邊![]() 上運動時,點
上運動時,點![]() 的橫坐標
的橫坐標![]() (單位長度)關于運動時間
(單位長度)關于運動時間![]() (秒)的函數圖象如圖2所示.
(秒)的函數圖象如圖2所示.
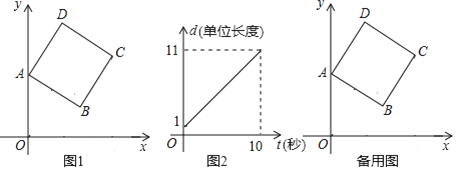
(1)正方形邊長![]() _____________,正方形頂點
_____________,正方形頂點![]() 的坐標為__________________;
的坐標為__________________;
(2)點![]() 開始運動時的坐標為__________,點
開始運動時的坐標為__________,點![]() 的運動速度為_________單位長度/秒;
的運動速度為_________單位長度/秒;
(3)當點![]() 運動時,點
運動時,點![]() 到
到![]() 軸的距離為
軸的距離為![]() ,求
,求![]() 與
與![]() 的函數關系式;
的函數關系式;
(4)當點![]() 運動時,過點
運動時,過點![]() 分別作
分別作![]() 軸,
軸,![]() 軸,垂足分別為點
軸,垂足分別為點![]() 、
、![]() ,且點
,且點![]() 位于點
位于點![]() 下方,
下方,![]() 與
與![]() 能否相似,若能,請直接寫出所有符合條件的
能否相似,若能,請直接寫出所有符合條件的![]() 的值;若不能,請說明理由.
的值;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知:∠MON=30o,點A1、A2、A3 在射線ON上,點B1、B2、B3…..在射線OM上,△A1B1A2. △A2B2A3、△A3B3A4……均為等邊三角形,若OA1=l,則△A6B6A7 的邊長為【 】

A.6 B.12 C.32 D.64
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近年來,“在初中數學教學候總使用計算器是否直接影響學生計算能力的發展”這一問題受到了廣泛關注,為此,某校隨機調查了n名學生對此問題的看法(看法分為三種:沒有影響,影響不大,影響很大),并將調查結果 繪制成如下不完整的統計表和扇形統計圖,根據統計圖表提供的信息,解答下列問題:
n名學生對使用計算器影響計算能力的發展看法人數統計表
看法 | 沒有影響 | 影響不大 | 影響很大 |
學生人數(人) | 40 | 60 | m |

(1)求n的值;
(2)統計表中的m= ;
(3)估計該校1800名學生中認為“影響很大”的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
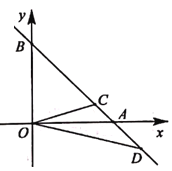
【題目】如圖,直線y=-x+2分別交x軸、y軸于點A,B,點D在BA的延長線上,OD的垂直平分線交線段AB于點C.若△OBC和△OAD的周長相等,則OD的長是( )
A. 2B. 2![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com