
【題目】如圖1,在△ABC中,∠A=30°,點P從點A出發以2cm/s的速度沿折線A—C—B運動,點Q從點A出發以a(cm/s)的速度沿AB運動,P,Q兩點同時出發,當某一點運動到點B時,兩點同時停止運動.設運動時間為x(s),△APQ的面積為y(cm2),y關于x的函數圖象由C1 , C2兩段組成,如圖2所示.
(1)求a的值;
(2)求圖2中圖象C2段的函數表達式;
(3)當點P運動到線段BC上某一段時△APQ的面積,大于當點P在線段AC上任意一點時△APQ的面積,求x的取值范圍.
【答案】
(1)
解:在圖1中,過P作PD⊥AB于D,∵∠A=30°,PA=2x,
∴PD=PA·sin30°=2x· ![]() =x,
=x,
∴y= ![]() =
= ![]() .
.
由圖象得,當x=1時,y= ![]() ,則
,則 ![]() =
= ![]() .
.
∴a=1.

(2)
解:當點P在BC上時(如圖2),PB=5×2-2x=10-2x.
∴PD=PB·sinB=(10-2x)·sinB,
∴y= ![]() AQ·PD=
AQ·PD= ![]() x·(10-2x)·sinB.
x·(10-2x)·sinB.
由圖象得,當x=4時,y= ![]() ,
,
∴ ![]() ×4×(10-8)·sinB=
×4×(10-8)·sinB= ![]() ,
,
∴sinB= ![]() .
.
∴y= ![]() x·(10-2x)·
x·(10-2x)· ![]() =
= ![]() .
.

(3)
解:由C1,C2的函數表達式,得 ![]() =
= ![]() ,
,
解得x1=0(舍去),x2=2,
由圖易得,當x=2時,函數y= ![]() 的最大值為y=
的最大值為y= ![]() .
.
將y=2代入函數y= ![]() ,得2=
,得2= ![]() .
.
解得x1=2,x2=3,
∴由圖象得,x的取值范圍是2<x<3.
【解析】(1)C1段的函數解析式是點P在AC線段時y與x的關系,由S= ![]() AQ·(AQ上的高),而AQ=ax,由∠A=30°,PA=2x,可過P作PD⊥AB于D,則PD=PA·sin30°=2x·
AQ·(AQ上的高),而AQ=ax,由∠A=30°,PA=2x,可過P作PD⊥AB于D,則PD=PA·sin30°=2x· ![]() =x,則可寫出y關于x的解析式,代入點(1,
=x,則可寫出y關于x的解析式,代入點(1, ![]() )即可解出;(2)作法與(1)同理,求出用sinB表示出PD,再寫出y與x的解析式,代入點(4,
)即可解出;(2)作法與(1)同理,求出用sinB表示出PD,再寫出y與x的解析式,代入點(4, ![]() ),即可求出sinB,即可解答;(3)題中表示在某x的取值范圍內C1<C2 , 即此時C2的y值大于C1的y值的最大值,由圖易得,當x=2時,函數y=
),即可求出sinB,即可解答;(3)題中表示在某x的取值范圍內C1<C2 , 即此時C2的y值大于C1的y值的最大值,由圖易得,當x=2時,函數y= ![]() 的最大值為y=
的最大值為y= ![]() .將y=2代入函數y=
.將y=2代入函數y= ![]() ,求出x的值,根據函數y=
,求出x的值,根據函數y= ![]() ,的開口向下,則可得x的取值范圍.
,的開口向下,則可得x的取值范圍.
【考點精析】關于本題考查的二次函數的圖象和二次函數的性質,需要了解二次函數圖像關鍵點:1、開口方向2、對稱軸 3、頂點 4、與x軸交點 5、與y軸交點;增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小才能得出正確答案.


科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC中,∠C=90°,AC=BC= ![]() ,將△ABC繞點A順時針方向旋轉60°到△AB′C′的位置,連接C′B.
,將△ABC繞點A順時針方向旋轉60°到△AB′C′的位置,連接C′B. 
(1)請你在圖中把圖補畫完整;
(2)求C′B的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學開展了“手機伴我健康行”主題活動.他們隨機抽取部分學生進行“手機使用目的”和“每周使用手機時間”的問卷調查,并繪制成如圖①②的統計圖。已知“查資料”人人數是40人。

請你根據以上信息解答以下問題
(1)在扇形統計圖中,“玩游戲”對應的圓心角度數是_______________。
(2)補全條形統計圖
(3)該校共有學生1200人,估計每周使用手機時間在2小時以上(不含2小時)的人數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某農場擬建一間矩形種牛飼養室,飼養室的一面靠現有墻(墻足夠長),已知計劃中的建筑材料可建圍墻的總長為為50m.設飼養室長為x(m),占地面積為y(m2).
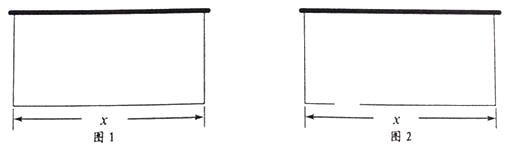
(1)如圖1,問飼養室長x為多少時,占地面積y最大?
(2)如圖2,現要求在圖中所示位置留2m寬的門,且仍使飼養室的占地面積最大。小敏說:“只要飼養室長比(1)中的長多2m就行了.”
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為做好食堂的服務工作,某學校食堂對學生最喜愛的菜肴進行了抽樣調查,下面試根據收集的數據繪制的統計圖(不完整):
(1)參加抽樣調查的學生數是______人,扇形統計圖中“大排”部分的圓心角是______°;
(2)把條形統計圖補充完整;
(3)若全校有3000名學生,請你根據以上數據估計最喜愛“烤腸”的學生人數.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列3×3網格圖都是由9個相同的小正方形組成,每個網格圖中有3個小正方形已涂上陰影,請在余下的6個空白小正方形中,按下列要求涂上陰影:
(1)選取1個涂上陰影,使4個陰影小正方形組成一個軸對稱圖形,但不是中心對稱圖形;
(2)選取1個涂上陰影,使4個陰影小正方形組成一個中心對稱圖形,但不是軸對稱圖形;
(3)選取2個涂上陰影,使5個陰影小正方形組成一個軸對稱圖形.
(請將三個小題依次作答在圖1、圖2、圖3中,均只需畫出符合條件的一種情形)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的口袋里裝有顏色不同的黃、白兩種顏色的球共5只,某學習小組做摸球實驗,將球攪勻后從中隨機摸出一個球記下顏色,再把它放回袋中,不斷重復![]()
![]() 下表是活動中的一組統計數據:
下表是活動中的一組統計數據:

(1)請估計:當n很大時,摸到白球的頻率將會接近______;(精確到0.1)
(2)試估算口袋中白種顏色的球有多少只?
(3)請你設計一個增(減)袋中白球或黃球球個數的方案,使得從袋中摸出一個球,這只球是黃球的概率大于是白球的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知四邊形ABCD是⊙O的內接四邊形,∠ABC=2∠D,連接OC、OA、AC. 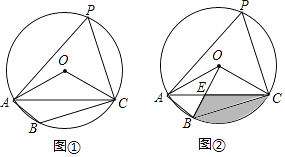
(1)如圖①,求∠OCA的度數;
(2)如圖②,連接OB、OB與AC相交于點E,若∠COB=90°,OC=2 ![]() ,求BC的長和陰影部分的面積.
,求BC的長和陰影部分的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com