
【題目】閱讀理解:
若一個整數能表示成a2+b2(a、b是整數)的形式,則稱這個數為“平和數”,例如5是“平和數”,因為5=22+1,再如,M=x2+2xy+2y2=(x+y)2+y2(x,y是整數),我們稱M也是“平和數”.
(1)請你寫一個小于5的“平和數”,并判斷34是否為“平和數”.
(2)已知S=x2+9y2+6x﹣6y+k(x,y是整數,k是常數,要使S為“平和數”,試求出符合條件的一個k值,并說明理由.
(3)如果數m,n都是“平和數”,試說明![]() 也是“平和數”.
也是“平和數”.
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AC≠BC,點M是邊AC上的動點.過點M作MN∥AB交BC于N,現將△MNC沿MN折疊,得到△MNP.若點P在AB上.則以MN為直徑的圓與直線AB的位置關系是 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
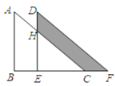
【題目】如圖,將直角三角形ABC沿著BC方向平移![]() cm得到直角三角形DEF,AB=5cm,BC=8cm,DH=2cm,那么圖中陰影部分的面積為____ cm 2.
cm得到直角三角形DEF,AB=5cm,BC=8cm,DH=2cm,那么圖中陰影部分的面積為____ cm 2.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=5,BC=3,將矩形ABCD繞點B按順時針方向旋轉得到矩形GBEF,點A落在矩形ABCD的邊CD上,連接CE,則CE的長是 . 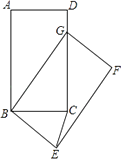
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在△ABC中,AB=AC=8,∠BAC=30°,將△ABC繞點A旋轉,使點B落在原△ABC的點C處,此時點C落在點D處,延長線段AD,交原△ABC的邊BC的延長線于點E,那么線段DE的長等于 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四邊形ADEF是正方形,點B、C分別在邊AD、AF上,此時BD=CF,BD⊥CF成立.
(1)當△ABC繞點A逆時針旋轉θ(0°<θ<90°)時,如圖2,BD=CF成立嗎?若成立,請證明,若不成立,請說明理由;
(2)當△ABC繞點A逆時針旋轉45°時,如圖3,延長BD交CF于點H.
①求證:BD⊥CF;
②當AB=2,AD=3 ![]() 時,求線段DH的長.
時,求線段DH的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中.四邊形![]() 是平行四邊形,其中
是平行四邊形,其中![]() 將
將![]() 在
在![]() 軸上順時針翻滾.如:第一次翻滾得到
軸上順時針翻滾.如:第一次翻滾得到![]() 第二次翻滾得到
第二次翻滾得到![]() ,···則第五次翻滾后,
,···則第五次翻滾后,![]() 點的對應點坐標為( )
點的對應點坐標為( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點M是正方形ABCD的邊BC上一點,連接AM,點E是線段AM上一點,∠CDE的平分線交AM延長線于點F.
(1)如圖1,若點E為線段AM的中點,BM:CM=1:2,BE=![]() ,求AB的長;
,求AB的長;
(2)如圖2,若DA=DE,求證:BF+DF=![]() AF.
AF.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,點O是邊AC上一個動點,過O作直線MN∥BC.設MN交∠ACB的平分線于點E,交∠ACB的外角平分線于點F.

(1)求證:OE=OF;
(2)若CE=12,CF=5,求OC的長;
(3)當點O在邊AC上運動到什么位置時,四邊形AECF是矩形?并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com