【題目】李明準備進行如下操作實驗，把一根長40 cm的鐵絲剪成兩段，并把每段首尾相連各圍成一個正方形．
(1)要使這兩個正方形的面積之和等于58 cm2，李明應該怎么剪這根鐵絲？
(2)李明認為這兩個正方形的面積之和不可能等于48 cm2，你認為他的說法正確嗎？請說明理由．
【答案】 (1) 李明應該把鐵絲剪成12 cm和28 cm的兩段；(2) 李明的說法正確，理由見解析.
【解析】試題分析：（1）設剪成的較短的這段為xcm，較長的這段就為（40﹣x）cm．就可以表示出這兩個正方形的面積，根據兩個正方形的面積之和等于58cm2建立方程求出其解即可；
（2）設剪成的較短的這段為mcm，較長的這段就為（40﹣m）cm．就可以表示出這兩個正方形的面積，根據兩個正方形的面積之和等于48cm2建立方程，如果方程有解就說明李明的說法錯誤，否則正確．
試題解析：設其中一段的長度為
cm，兩個正方形面積之和為
cm2，則
，
（其中
），當
時，
，解這個方程，得
，
，∴應將之剪成12cm和28cm的兩段；
（2）兩正方形面積之和為48時，
，
，∵
， ∴該方程無實數解，也就是不可能使得兩正方形面積之和為48cm2，李明的說法正確．
科目：初中數學 來源： 題型：
【題目】“不覽夜景，味道重慶．”乘游船也有兩江，猶如在星河中暢游，是一個近距離認識重慶的最佳窗口．“兩江號”游輪經過核算，每位游客的接待成本為30元．根據市場調查，同一時段里，票價為40元時，每晚將售出船票600張，而票價每漲1元，就會少售出10張船票．
（1）若該游輪每晚獲得10000元利潤的同時，適當控制游客人數，保持應有的服務水準，則票價應定為多少元？
（2）春節期間，工商管理部門規定游輪船票單價不能低于44元，同時該游輪為提高市場占有率，決定每晚售出船票數量不少于540張，則票價應定為多少元，才能使每晚獲得的利潤最多？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，四邊形ABCD是平行四邊形，點A、B在x軸上，點C、D在第二象限，點M是BC中點.已知AB=6，AD=8，∠DAB=60°，點B的坐標為（-6，0）．
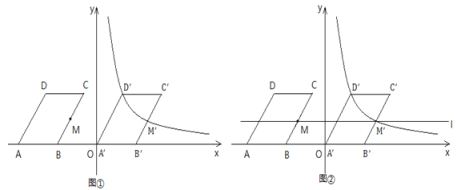
（1）求點D和點M的坐標；
（2）如圖①，將□ABCD沿著x軸向右平移a個單位長度，點D的對應點
和點M的對應點
恰好在反比例函數
（x>0）的圖像上，請求出a的值以及這個反比例函數的表達式；
（3）如圖②，在（2）的條件下，過點M，作直線l，點P是直線l上的動點，點Q是平面內任意一點，若以
，P、Q為頂點的四邊形是矩形，請直接寫出所有滿足條件的點Q的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，一動點從原點O出發，按向上、向右、向下、向右的方向不斷地移動，每次移動1個單位長度，得到點A1(0，1)，A2(1，1)，A3(1，0)，A4(2，0)，…，那么點A2 019的坐標為________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知∠AOB，以O為圓心，以任意長為半徑作弧，分別交OA，OB于F，E兩點，再分別以E，F為圓心，大于
EF長為半徑作圓弧，兩條圓弧交于點P，作射線OP，過點F作FD∥OB交OP于點D.
(1)若∠OFD＝116°，求∠DOB的度數；
(2)若FM⊥OD，垂足為M，求證：△FMO≌△FMD.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，一個智能機器人接到如下指令：從原點O出發，按向右，向上，向右，向下的方向依次不斷移動，每次移動1m．其行走路線如圖所示，第1次移動到A1，第2次移動到A2，…，第n次移動到An．則△OA2A2018的面積是（ ）
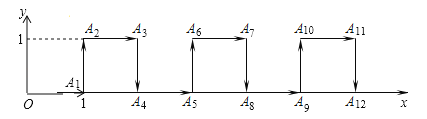
A. 504m2 B. 
m2 C. 
m2 D. 1009m2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
