
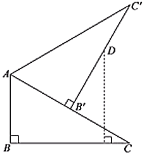
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,將
,將![]() 繞點
繞點![]() 旋轉(zhuǎn)得到
旋轉(zhuǎn)得到![]() ,使點
,使點![]() 的對應(yīng)點
的對應(yīng)點![]() 落在
落在![]() 上,在
上,在![]() 上取點
上取點![]() ,使
,使![]() ,那么點
,那么點![]() 到
到![]() 的距離等于( ).
的距離等于( ).
A.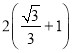 B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
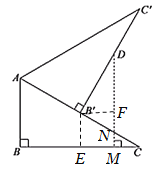
根據(jù)旋轉(zhuǎn)的性質(zhì)和30°角的直角三角形的性質(zhì)可得![]() 的長,進而可得
的長,進而可得![]() 的長,過點D作DM⊥BC于點M,過點
的長,過點D作DM⊥BC于點M,過點![]() 作
作![]() 于點E,
于點E,![]() 于點F,如圖,則四邊形
于點F,如圖,則四邊形![]() 是矩形,解Rt△
是矩形,解Rt△![]() 可得
可得![]() 的長,即為FM的長,根據(jù)三角形的內(nèi)角和易得
的長,即為FM的長,根據(jù)三角形的內(nèi)角和易得![]() ,然后解Rt△
,然后解Rt△![]() 可求出DF的長,進一步即可求出結(jié)果.
可求出DF的長,進一步即可求出結(jié)果.
解:在![]() 中,∵
中,∵![]() ,
,![]() ,
,
∴AC=2AB=4,
∵將![]() 繞點
繞點![]() 旋轉(zhuǎn)得到
旋轉(zhuǎn)得到![]() ,使點
,使點![]() 的對應(yīng)點
的對應(yīng)點![]() 落在
落在![]() 上,
上,
∴![]() ,
,
∴![]() ,
,
過點D作DM⊥BC于點M,過點![]() 作
作![]() 于點E,
于點E,![]() 于點F,交AC于點N,如圖,則四邊形
于點F,交AC于點N,如圖,則四邊形![]() 是矩形,
是矩形,
∴![]() ,
,
在Rt△![]() 中,
中,![]() ,∴FM=1,
,∴FM=1,
∵![]() ,
,
∴![]() ,
,
在Rt△![]() 中,
中,![]() ,
,
∴![]() ,
,
即點![]() 到
到![]() 的距離等于
的距離等于![]() .
.
故選:D.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】圖1,圖2是兩張形狀、大小完全相同的方格紙,方格紙中的每個小正方形的邊長均為1,線段AB的兩個端點均在小正方形的頂點上.
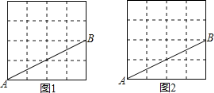
(1)在圖1中畫出以AB為底邊的等腰直角三角形ABC,點C在小正方形的頂點上;
(2)在圖2中畫出以AB為腰的等腰三角形ABD,點D在小正方形的頂點上,且△ABD的面積為8.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,已知拋物線
中,已知拋物線![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() .
.
(1)求拋物線的函數(shù)表達式
(2)如圖1,點![]() 為第四象限拋物線上一點,連接
為第四象限拋物線上一點,連接![]() ,
,![]() 交于點
交于點![]() ,連接
,連接![]() ,記
,記![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 的最大值;
的最大值;
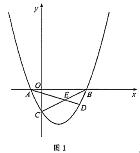
(3)如圖2,連接![]() ,
,![]() ,過點
,過點![]() 作直線
作直線![]() ,點
,點![]() ,
,![]() 分別為直線和拋物線上的點.試探究:在第一象限是否存在這樣的點
分別為直線和拋物線上的點.試探究:在第一象限是否存在這樣的點![]() ,
,![]() ,使
,使![]() .若存在,請求出所有符合條件的點
.若存在,請求出所有符合條件的點![]() 的坐標(biāo);若不存在,請說明理由.
的坐標(biāo);若不存在,請說明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,有四張正面標(biāo)有數(shù)字![]() ,背面顏色一樣的卡片,正面朝下放在桌面上,小紅從中隨機抽取一張卡片記下數(shù)字,再從余下的卡片中隨機抽取一張卡片記下數(shù)字.
,背面顏色一樣的卡片,正面朝下放在桌面上,小紅從中隨機抽取一張卡片記下數(shù)字,再從余下的卡片中隨機抽取一張卡片記下數(shù)字.
(1)第一次抽到數(shù)字2的卡片的概率是 ;
(2)設(shè)第一次抽到的數(shù)字為![]() ,第二次抽到的數(shù)字為
,第二次抽到的數(shù)字為![]() ,點
,點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,請用樹狀圖或列表法求點
,請用樹狀圖或列表法求點![]() 在第三象限的概率.
在第三象限的概率.
![]()
![]()
![]()
![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
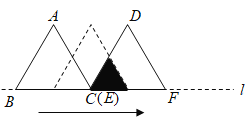
【題目】如圖![]() 和
和![]() 都是邊長為
都是邊長為![]() 的等邊三角形,它們的邊
的等邊三角形,它們的邊![]() 在同一條直線
在同一條直線![]() 上,點
上,點![]() ,
,![]() 重合,現(xiàn)將
重合,現(xiàn)將![]() 沿著直線
沿著直線![]() 向右移動,直至點
向右移動,直至點![]() 與
與![]() 重合時停止移動.在此過程中,設(shè)點移動的距離為
重合時停止移動.在此過程中,設(shè)點移動的距離為![]() ,兩個三角形重疊部分的面積為
,兩個三角形重疊部分的面積為![]() ,則
,則![]() 隨
隨![]() 變化的函數(shù)圖像大致為( )
變化的函數(shù)圖像大致為( )
A. 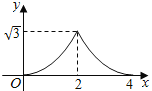 B.
B. 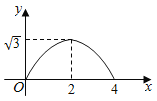
C. 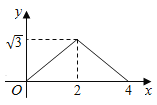 D.
D. 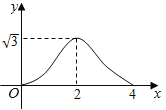
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,小瑩在數(shù)學(xué)綜合實踐活動中,利用所學(xué)的數(shù)學(xué)知識對某小區(qū)居民樓AB的高度進行測量.先測得居民樓AB與CD之間的距離AC為35m,后站在M點處測得居民樓CD的頂端D的仰角為45°.居民樓AB的頂端B的仰角為55°.已知居民樓CD的高度為16.6m,小瑩的觀測點N距地面1.6m.求居民樓AB的高度(精確到1m).(參考數(shù)據(jù):sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
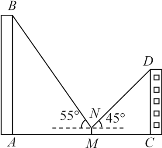
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1是一手機支架,其中AB=8cm,底座CD=1cm,當(dāng)點A正好落在桌面上時如圖2所示,∠ABC=80°,∠A=60°.
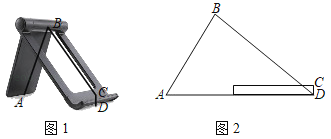
(1)求點B到桌面AD的距離;
(2)求BC的長.(結(jié)果精確到0.1cm;參考數(shù)據(jù):sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABE中,C,D是邊BE上的兩點,有下面四個關(guān)系式:(1)AB=AE,(2)BC=DE,(3)AC=AD,(4)∠BAC=∠EAD.請用其中兩個作為已知條件,余下兩個作為求證的結(jié)論,寫出你的已知和求證,并證明.
已知:
求證:
證明:
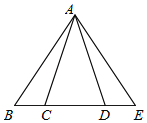
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為了迎接“五一”小長假的購物高峰.某服裝專賣店老板小王準備購進甲、乙兩種夏季服裝.其中甲種服裝每件的成本價比乙種服裝的成本價多20元,甲種服裝每件的售價為240元比乙種服裝的售價多80元.小王用4000元購進甲種服裝的數(shù)量與用3200元購進乙種服裝的數(shù)量相同.
(1)甲種服裝每件的成本是多少元?
(2)要使購進的甲、乙兩種服裝共200件的總利潤(利潤=售價-進價)不少于21100元,且不超過21700元,問小王有幾種進貨方案?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com